Opa, olha eu aqui de novo !!
Vamos resolver mais essa campeão ?? Então, vamos lá...
Primeiramente vamos definir as variáveis, como sempre, chamaremos de x o número de crianças e y o total de bolas, ok ?!
"...Certo numeros de bolas foi repartido entre várias crianças,cabendo a cada uma 5 bolas(sic)...", para mim, essa frase diz que se cada criança recebe 5 bolas, não sobra nada, logo teremos:

"...Se tivessemos dado apenas 2 bolas a cada uma,poderiamos ter presenteado a mais 31 crianças e ainda sobraria uma bola(sic)...", bem, aqui temos a seguinte situação, se entregássemos 2 bolas para cada criança ainda poderíamos presentear mais 31 crianças e sobraria uma bola.. Isto é, dando 2 bolas para todas as crianças e mais 31, sobra 1 bola, logo:

Igualando as equações, teremos:

Achamos

, isto é, temos 21 crianças, logo o total de bolas será:

Espero ter ajudado...
Abs,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
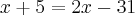

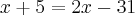




 , isto é, temos 21 crianças, logo o total de bolas será:
, isto é, temos 21 crianças, logo o total de bolas será:




 , avisa que eu resolvo.
, avisa que eu resolvo.

