


nietzsche escreveu:Boa tarde.
Seja Gn = {x é real: -1/n < x < 1+1/n } , onde n é natural.
A interseção dos conjuntos Gn é o conjunto F = {x é real: 0<= x <= 1}.
Se x pertence a interseção dos Gn, então ele pertence a todos Gn, para todo n. Mas como explicar que o 0 e o 1 sãos as cotas que limitam o intervalo de F?
Agradeço desde já.

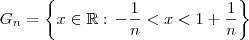 . O que nós queremos é determinar F tal que
. O que nós queremos é determinar F tal que 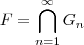 . Eu pensei assim: se você tomar o limite dos dois lados da desigualdade, com
. Eu pensei assim: se você tomar o limite dos dois lados da desigualdade, com 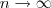 , veja que o único conjunto que pertence a todos é realmente
, veja que o único conjunto que pertence a todos é realmente 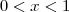 , pois
, pois 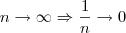 . Isto é mais uma idéia intuitiva, não considero isso como um argumento rigoroso.
. Isto é mais uma idéia intuitiva, não considero isso como um argumento rigoroso.


![]0,1[ \subset [0,1] ]0,1[ \subset [0,1]](/latexrender/pictures/7ad02b7ee807696544aad5b57470d4ba.png) . Talvez para ficar mais elegante.
. Talvez para ficar mais elegante.











Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.