 por LBT » Qui Jan 13, 2011 09:05
por LBT » Qui Jan 13, 2011 09:05
boas,
Como faço para calcular
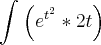
Cmps
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por MarceloFantini » Qui Jan 13, 2011 11:11
por MarceloFantini » Qui Jan 13, 2011 11:11
Use substituição simples, fazendo

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LBT » Qui Jan 13, 2011 21:26
por LBT » Qui Jan 13, 2011 21:26
Fantini escreveu:Use substituição simples, fazendo

.
Desculpe, não entendi a ideia :S
Como assim

?!
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por LBT » Sex Jan 14, 2011 07:03
por LBT » Sex Jan 14, 2011 07:03
Fantini escreveu:Você aprendeu mudança de variável na integral? É isso que você tem que fazer:

. Então a integral fica:
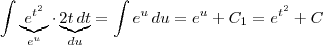
Ja percebi, obrigado! Tinha aqui 2 resolvidos dessa maneira, mas nc tinha percebido o porque! Agora percebi, obrigado
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DERIVAR ou INTEGRAR
por DESESPERADO » Qui Nov 11, 2010 14:14
- 15 Respostas
- 13429 Exibições
- Última mensagem por andrefahl

Sex Nov 12, 2010 17:45
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar esta função?
por Ibraim » Ter Mar 06, 2012 17:19
- 2 Respostas
- 2788 Exibições
- Última mensagem por Ibraim

Ter Mar 06, 2012 19:00
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar essa derivada: ?2/(3x²+2)dx
por Therodrigou » Ter Set 18, 2018 03:08
- 3 Respostas
- 7977 Exibições
- Última mensagem por Gebe

Ter Set 18, 2018 15:36
Cálculo: Limites, Derivadas e Integrais
-
- [Urgente] Integrar uma aceleração dada
por grey » Qua Fev 15, 2017 19:08
- 1 Respostas
- 2204 Exibições
- Última mensagem por adauto martins

Qui Fev 16, 2017 17:12
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - como integrar essa função?
por vinik1 » Seg Dez 05, 2011 15:53
- 2 Respostas
- 2930 Exibições
- Última mensagem por vinik1

Seg Dez 05, 2011 16:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
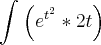

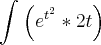


.
 ?!
?!
 . Então a integral fica:
. Então a integral fica: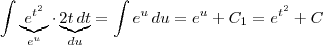


. Então a integral fica:
