 por douglasjro » Qui Jan 13, 2011 12:20
por douglasjro » Qui Jan 13, 2011 12:20
(UFG) - Para que a soma das raízes da equação
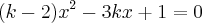
seja igual ao seu produto devemos ter?
Resposta:
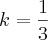
Obriagdo.
Douglas Oliveira
-
douglasjro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Jan 10, 2011 18:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Processos Gerenciais
- Andamento: cursando
 por VtinxD » Qui Jan 13, 2011 14:45
por VtinxD » Qui Jan 13, 2011 14:45
Assim como no seu outro post ,esse exercicio é uma questão que envolve as relações de soma e produto da equação do segundo grau,onde:
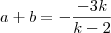
e
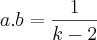
.Sua forma mais geral seria:
Para toda equação da forma
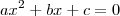
,vale as relações
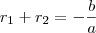
e
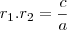
se e somente se
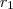
e
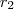
são raizes da equação.
Estas relações fazem parte das relações de Girard.
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por douglasjro » Sex Jan 14, 2011 13:27
por douglasjro » Sex Jan 14, 2011 13:27
Muito obrigado consegui resolver. 
Douglas Oliveira
-
douglasjro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Jan 10, 2011 18:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Processos Gerenciais
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3158 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4156 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3437 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6503 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2274 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
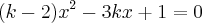 seja igual ao seu produto devemos ter?
seja igual ao seu produto devemos ter?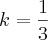

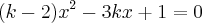 seja igual ao seu produto devemos ter?
seja igual ao seu produto devemos ter?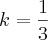

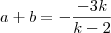 e
e 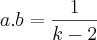 .Sua forma mais geral seria:
.Sua forma mais geral seria: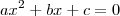 ,vale as relações
,vale as relações 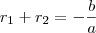 e
e 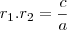 se e somente se
se e somente se 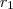 e
e 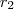 são raizes da equação.
são raizes da equação.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.