 por PedroSantos » Dom Jan 09, 2011 16:38
por PedroSantos » Dom Jan 09, 2011 16:38
A equação reduzida da circunferência no plano é dada por
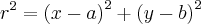
em que (
a,
b) é o centro da circunferência.
Questão:
Dada uma circunferência no plano, com raio igual a 3 e um ponto
P pertencente à circunferência de coordenadas
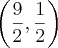
, calcule o par ordenado correspondende ao centro da circunferência.
Eu ainda comecei por aplicar a equação, mas perante duas variáveis ( a e b), concluí rapidamente que existem inúmeras soluções.
Existe um número ilimitado de circunferências, que tendo r=3, passam pelo ponto P.
Estarei correcto?
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por MarceloFantini » Dom Jan 09, 2011 22:34
por MarceloFantini » Dom Jan 09, 2011 22:34
Concordo, você só terá uma equação e duas incógnitas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Pedro123 » Seg Jan 10, 2011 14:55
por Pedro123 » Seg Jan 10, 2011 14:55
Pedro, seguinte, pelo o que eu entendi do problema, concordo com vc, havéra um número infinito de pontos, porém, não são pontos aleatórios, serão pontos que pertencerão à uma circunferência também, tente desenvolver a equação com os pontos dados, vc chegará à equação de uma circunferência.
abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Guill » Sáb Fev 25, 2012 12:18
por Guill » Sáb Fev 25, 2012 12:18
Considere uma circunferência de raio r. Sua equação é dada por:
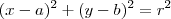
, onde (a ; b) representa as coordenadas do centro dessa circunferência.
No caso da sua circunferência, teríamos um raio r = 3 e as coordenadas
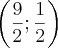
, que pertencem à circunferência:
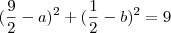
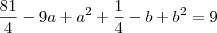
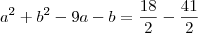
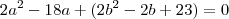
Desenvolvendo essa equação quadrática, teremos o valor a em função de b, No entanto, calcularemos os valores do delta para encontrar os valores possíveis de b:
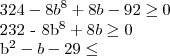
![b = \frac{-1 + \sqrt[]{117}}{2} b = \frac{-1 + \sqrt[]{117}}{2}](/latexrender/pictures/b3d22a058bb3047a28e5d9711cff4d7b.png)
![b = \frac{-1 - \sqrt[]{117}}{2} b = \frac{-1 - \sqrt[]{117}}{2}](/latexrender/pictures/eba4ae7a8dd441ef7443a4f547f96a5c.png)
Dessa forma, o valor de y do centro da circunferência varia entre esses dois valores. Temos, portanto, infinitas circunferências. Se quer imaginar porque isso acontece, basta escolher uma circunferência de raio 3 que possui esse ponto e arrastar ela sem tirar o ponto da superfície. O mais interessante é que o centro faz uma circunferência com esse movimento.
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação da Circunferência
por Cleyson007 » Qui Abr 08, 2010 15:35
- 1 Respostas
- 11153 Exibições
- Última mensagem por davi_11

Dom Abr 11, 2010 13:46
Geometria Analítica
-
- Equação da circunferência
por Andreza » Sáb Fev 25, 2012 09:43
- 1 Respostas
- 1511 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 11:43
Geometria Analítica
-
- Equação na Circunferência
por Fernandobertolaccini » Dom Mai 11, 2014 14:48
- 1 Respostas
- 1245 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:26
Geometria Analítica
-
- Equação da circunferencia
por brunoguim05 » Qua Mai 28, 2014 15:20
- 1 Respostas
- 1282 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:15
Equações
-
- Equação da circunferência
por YuriFreire » Seg Ago 25, 2014 23:22
- 2 Respostas
- 1376 Exibições
- Última mensagem por YuriFreire

Ter Ago 26, 2014 22:30
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
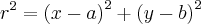
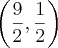 , calcule o par ordenado correspondende ao centro da circunferência.
, calcule o par ordenado correspondende ao centro da circunferência.




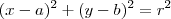 , onde (a ; b) representa as coordenadas do centro dessa circunferência.
, onde (a ; b) representa as coordenadas do centro dessa circunferência.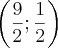 , que pertencem à circunferência:
, que pertencem à circunferência: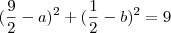
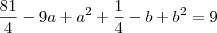
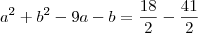
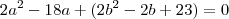
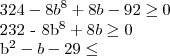
![b = \frac{-1 + \sqrt[]{117}}{2} b = \frac{-1 + \sqrt[]{117}}{2}](/latexrender/pictures/b3d22a058bb3047a28e5d9711cff4d7b.png)
![b = \frac{-1 - \sqrt[]{117}}{2} b = \frac{-1 - \sqrt[]{117}}{2}](/latexrender/pictures/eba4ae7a8dd441ef7443a4f547f96a5c.png)
