MDC = Maior Divisor Comum
O 2 é de fato, divisor de A, B e C, mas não é o maior. Mas olhemos apenas para o 2, porque esses 3 números tem em comum apenas potências com essa base.
Para determinar o MDC, a gente pega o fator com o menor expoente dessa base em comum.
No caso, o fator é 2? e está no B. Portanto, o MDC entre eles é 2? = 16.
MMC = Mínimo Múltiplo Comum.
Temos que pegar a base dos fatores presentes em todos os números:
2, 3, 5 e 7.
Depois, temos que ver em qual dos números, essa base apresenta o MAIOR expoente. Afinal, o mmc é múltiplo de todos. Se pegarmos um expoente menor do que o máximo apresentado na fatoração, ele não será múltiplo de um dos números. E se pegarmos um expoente maior do que o máximo obtido na fatoração, ele será múltiplo, porém não será o Mínimo.
Com isso, pegamos:
2?, 3?, 5?, 7²
Multiplicamos esses fatores e essa é a resposta: 2? . 3? . 5? . 7².
Você só errou no expoente do 7. Espero que tenha entendido o conceito.
E o número é grande mesmo. Acho que a resposta fatorada é o suficiente.

Boa prova pro seu filho e qualquer dúvida, venha aqui no fórum novamente.
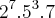
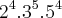
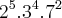
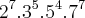 só que isso dá um resultado muito grande.
só que isso dá um resultado muito grande.

 Boa prova pro seu filho e qualquer dúvida, venha aqui no fórum novamente.
Boa prova pro seu filho e qualquer dúvida, venha aqui no fórum novamente.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)