 por vyhonda » Sáb Nov 20, 2010 12:39
por vyhonda » Sáb Nov 20, 2010 12:39
FGV - Uma sala tem 10 portas. Calcular o número de maneiras diferentes que essa sala pode ser aberta.
Valeu pela ajuda!
-
vyhonda
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jan 17, 2010 20:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais - Unesp
- Andamento: cursando
 por 0 kelvin » Sáb Nov 20, 2010 22:59
por 0 kelvin » Sáb Nov 20, 2010 22:59
Parece um problema de lógica de concursos público

Primeiro achei q era 10!, mas não é. Procurei e entendi um raciocínio manual q é:
A soma de 10 combinações uma por uma. De quantas maneiras diferentes podemos abrir uma porta? Duas? .... nove? dez?
A outra maneira é
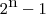
onde n é o número de portas. É a mesma fórmula do número de movimentos do brinquedo "Torres de Hanói".
Uma porta tem duas condições aberta ou fechada. 10 portas em conjunto tem então
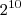
condições de aberto ou fechado, incluindo todas fechadas, que é o único caso da sala estar fechada sem nenhuma porta aberta.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por vyhonda » Dom Nov 21, 2010 01:37
por vyhonda » Dom Nov 21, 2010 01:37
Valeu Kelvin
Essa linha de raciocínio é interessante... não havia pensado nisso
a resp é mesmo
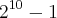
!
tenks!
-
vyhonda
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jan 17, 2010 20:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais - Unesp
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Combinatória-analise combinatoria
por heloisacarvalho83 » Seg Fev 27, 2012 22:40
- 1 Respostas
- 2889 Exibições
- Última mensagem por Livia000

Qua Mai 23, 2012 00:26
Estatística
-
- combinatória
por Adilson » Sex Ago 28, 2009 13:50
- 1 Respostas
- 2144 Exibições
- Última mensagem por Molina

Sex Ago 28, 2009 21:19
Estatística
-
- Combinatória
por 2137RF » Sex Out 09, 2009 11:25
- 4 Respostas
- 3485 Exibições
- Última mensagem por shirata

Qui Nov 26, 2009 06:38
Estatística
-
- combinatória
por apoliveirarj » Dom Jul 25, 2010 16:50
- 2 Respostas
- 4883 Exibições
- Última mensagem por apoliveirarj

Qui Ago 05, 2010 19:27
Estatística
-
- Combinatória
por apoliveirarj » Sáb Ago 07, 2010 12:23
- 2 Respostas
- 2469 Exibições
- Última mensagem por apoliveirarj

Sex Ago 13, 2010 15:55
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




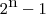 onde n é o número de portas. É a mesma fórmula do número de movimentos do brinquedo "Torres de Hanói".
onde n é o número de portas. É a mesma fórmula do número de movimentos do brinquedo "Torres de Hanói".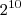 condições de aberto ou fechado, incluindo todas fechadas, que é o único caso da sala estar fechada sem nenhuma porta aberta.
condições de aberto ou fechado, incluindo todas fechadas, que é o único caso da sala estar fechada sem nenhuma porta aberta.
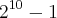 !
!

 .
.



