 por gustavowelp » Sex Nov 19, 2010 07:22
por gustavowelp » Sex Nov 19, 2010 07:22
Não entendi muito bem esta questão, principalmente o resultado:
Combinando-se os algarismos 1, 2, 3, 7 e 9 entre si, obtém-se:
A resposta é: 20 números.
Fiz arranjo, mas aí daria 120 números... A(5,5) = 5!/0! = 5!/1
Obrigado!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 13:28
por alexandre32100 » Sex Nov 19, 2010 13:28
Realmente, Gustavo, também cheguei a esta conclusão. Além do mais, são

números de cinco algarismos.
Revise o problema, pode ser que ele peça
os números de dois algarismos. Daí sim teríamos
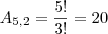
números.
-
alexandre32100
-
 por gustavowelp » Sex Nov 19, 2010 13:36
por gustavowelp » Sex Nov 19, 2010 13:36
Obrigado!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Arranjo ou combinação?
por cristina » Sex Ago 27, 2010 11:41
- 3 Respostas
- 2325 Exibições
- Última mensagem por profmatematica

Sáb Ago 28, 2010 05:08
Estatística
-
- Arranjo ou combinação??
por matpet92 » Dom Fev 12, 2012 12:40
- 2 Respostas
- 1452 Exibições
- Última mensagem por matpet92

Dom Fev 12, 2012 17:49
Estatística
-
- Arranjo ou Combinação?
por leomjr » Dom Ago 23, 2015 18:51
- 3 Respostas
- 2976 Exibições
- Última mensagem por leomjr

Qui Set 03, 2015 23:15
Análise Combinatória
-
- [Combinação de Numeros]Combinação até chegar em outro
por moacirrf » Dom Set 30, 2012 15:51
- 0 Respostas
- 1790 Exibições
- Última mensagem por moacirrf

Dom Set 30, 2012 15:51
Análise Combinatória
-
- Arranjo
por Pri Ferreira » Qua Mar 21, 2012 13:34
- 3 Respostas
- 2510 Exibições
- Última mensagem por LuizAquino

Seg Abr 09, 2012 23:30
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 números de cinco algarismos.
números de cinco algarismos.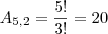 números.
números.

 .
.



