 por fttofolo » Sex Nov 19, 2010 11:05
por fttofolo » Sex Nov 19, 2010 11:05
prove que
![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)
-
fttofolo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Sex Nov 19, 2010 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Sex Nov 19, 2010 13:18
por alexandre32100 » Sex Nov 19, 2010 13:18
![\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)} \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)}](/latexrender/pictures/91f20857c23163d36edb2002d843de19.png)
Se elevarmos as duas expressões ao cubo temos:
![\left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1 \left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1](/latexrender/pictures/a150e09712eb83b51a7b32a12460efcb.png)
É bom lembrar que
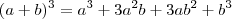
.
Aplicando isso à equação do problema:
![\\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5} \\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5}](/latexrender/pictures/df85e2bfa13d79b2e394027c3f5c51f5.png)
![\text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1 \text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1](/latexrender/pictures/24ade9849a5c6a358ec8ebb6d2d859cd.png)
, assim:
![4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right) 4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)](/latexrender/pictures/3ad2d56054fec5cc2e822b2e30075522.png)
Pela HI,

, cqd.
-
alexandre32100
-
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)


![\sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1 \sqrt[3]{2+\sqrt[2]{5}}+\sqrt[3]{2-\sqrt[2]{5}}=1](/latexrender/pictures/c1b67342a01ff8ef2ee26a2e4aa90a75.png)

![\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)} \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} \text{ (HI)}](/latexrender/pictures/91f20857c23163d36edb2002d843de19.png)
![\left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1 \left ( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right )^3=1^3=1](/latexrender/pictures/a150e09712eb83b51a7b32a12460efcb.png)
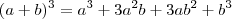 .
.![\\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5} \\2+\sqrt{5}+3\cdot\sqrt[3]{(2+\sqrt{5})(2+\sqrt{5})(2-\sqrt{5})}+3\cdot\sqrt[3]{(2+\sqrt{5})(2-\sqrt{5})(2-\sqrt{5})}+2-\sqrt{5}](/latexrender/pictures/df85e2bfa13d79b2e394027c3f5c51f5.png)
![\text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1 \text{Obs: } (2+\sqrt{5})(2-\sqrt{5})=2^2-5=-1 \text{ e }\sqrt[3]{-1}=-1](/latexrender/pictures/24ade9849a5c6a358ec8ebb6d2d859cd.png) , assim:
, assim:![4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right) 4+3\cdot\sqrt[3]{(2+\sqrt{5})(-1)}+3\cdot\sqrt[3]{(2-\sqrt{5})(-1)}=4-3\cdot\left(\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right)](/latexrender/pictures/3ad2d56054fec5cc2e822b2e30075522.png)
 , cqd.
, cqd.