 por VtinxD » Seg Nov 15, 2010 14:33
por VtinxD » Seg Nov 15, 2010 14:33
Perceba que no triângulo FED, retângulo, se usarmos o seno do angulo DFE:
![Sen(60°)=\frac{\sqrt[2]{3}}{2}=\frac{ED}{FD}\Rightarrow FD=\frac{2.ED}{\sqrt[2]{3}}\Rightarrow FD=\frac{2.(4\sqrt[2]{3})}{\sqrt[2]{3}}\Rightarrow FD=8 Sen(60°)=\frac{\sqrt[2]{3}}{2}=\frac{ED}{FD}\Rightarrow FD=\frac{2.ED}{\sqrt[2]{3}}\Rightarrow FD=\frac{2.(4\sqrt[2]{3})}{\sqrt[2]{3}}\Rightarrow FD=8](/latexrender/pictures/bfdac01f6fe473deaec511aa53f07fcc.png)
Sendo FD o ponto médio:
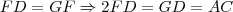
.Utilizando a projeção de F no segmento AC, temos um triângulo retângulo,FF'B.Como F' é projeção de F em AC ele também é ponto médio.Logo:
!['FB=FD-BC\Rightarrow 'FB=8-2\sqrt[2]{3} 'FB=FD-BC\Rightarrow 'FB=8-2\sqrt[2]{3}](/latexrender/pictures/53f2fcb659cdcb3438415b46b2e6038e.png)
.Como o angulo F'FD é igual a 90° ,temos:
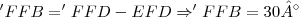
.Agora utilizando a tangente de F'FB:
![Tg(30°)=\frac{\sqrt[2]{3}}{3}=\frac{'FB}{F'F}\Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}} \Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}}.\frac{\sqrt[2]{3}}{\sqrt[2]{3}}\Rightarrow F'F='FB.\sqrt[2]{3} Tg(30°)=\frac{\sqrt[2]{3}}{3}=\frac{'FB}{F'F}\Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}} \Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}}.\frac{\sqrt[2]{3}}{\sqrt[2]{3}}\Rightarrow F'F='FB.\sqrt[2]{3}](/latexrender/pictures/655ca1d4a8fafdfabf2f4d52f03b13c4.png)
.É facil perceber que FF' é igual a GA e DC.
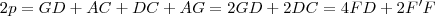
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por GeRmE » Seg Nov 15, 2010 15:51
por GeRmE » Seg Nov 15, 2010 15:51
obrigado amigo
-

GeRmE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Out 29, 2010 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estidante de medicina
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Perimetro
por Robinho » Sáb Jan 14, 2012 14:41
- 2 Respostas
- 1641 Exibições
- Última mensagem por Robinho

Sáb Jan 14, 2012 14:55
Sistemas de Equações
-
- Perímetro
por Ariel » Qui Nov 13, 2014 15:52
- 2 Respostas
- 1440 Exibições
- Última mensagem por Ariel

Qui Nov 13, 2014 22:18
Geometria Plana
-
- perimetro e area
por karenblond » Qui Mar 25, 2010 14:33
- 2 Respostas
- 2511 Exibições
- Última mensagem por karenblond

Qui Mar 25, 2010 17:14
Geometria Plana
-
- Perímetro do triângulo
por maria cleide » Sáb Mai 28, 2011 16:49
- 3 Respostas
- 3922 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 19:55
Geometria Plana
-
- Perímetro do triângulo
por leticiadelduque » Dom Ago 21, 2011 12:02
- 2 Respostas
- 1739 Exibições
- Última mensagem por leticiadelduque

Dom Ago 21, 2011 17:02
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![Sen(60°)=\frac{\sqrt[2]{3}}{2}=\frac{ED}{FD}\Rightarrow FD=\frac{2.ED}{\sqrt[2]{3}}\Rightarrow FD=\frac{2.(4\sqrt[2]{3})}{\sqrt[2]{3}}\Rightarrow FD=8 Sen(60°)=\frac{\sqrt[2]{3}}{2}=\frac{ED}{FD}\Rightarrow FD=\frac{2.ED}{\sqrt[2]{3}}\Rightarrow FD=\frac{2.(4\sqrt[2]{3})}{\sqrt[2]{3}}\Rightarrow FD=8](/latexrender/pictures/bfdac01f6fe473deaec511aa53f07fcc.png)
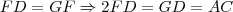 .Utilizando a projeção de F no segmento AC, temos um triângulo retângulo,FF'B.Como F' é projeção de F em AC ele também é ponto médio.Logo:
.Utilizando a projeção de F no segmento AC, temos um triângulo retângulo,FF'B.Como F' é projeção de F em AC ele também é ponto médio.Logo:!['FB=FD-BC\Rightarrow 'FB=8-2\sqrt[2]{3} 'FB=FD-BC\Rightarrow 'FB=8-2\sqrt[2]{3}](/latexrender/pictures/53f2fcb659cdcb3438415b46b2e6038e.png) .Como o angulo F'FD é igual a 90° ,temos:
.Como o angulo F'FD é igual a 90° ,temos: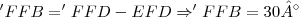 .Agora utilizando a tangente de F'FB:
.Agora utilizando a tangente de F'FB:![Tg(30°)=\frac{\sqrt[2]{3}}{3}=\frac{'FB}{F'F}\Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}} \Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}}.\frac{\sqrt[2]{3}}{\sqrt[2]{3}}\Rightarrow F'F='FB.\sqrt[2]{3} Tg(30°)=\frac{\sqrt[2]{3}}{3}=\frac{'FB}{F'F}\Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}} \Rightarrow F'F=\frac{3.'FB}{\sqrt[2]{3}}.\frac{\sqrt[2]{3}}{\sqrt[2]{3}}\Rightarrow F'F='FB.\sqrt[2]{3}](/latexrender/pictures/655ca1d4a8fafdfabf2f4d52f03b13c4.png) .É facil perceber que FF' é igual a GA e DC.
.É facil perceber que FF' é igual a GA e DC.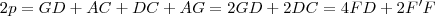




 , avisa que eu resolvo.
, avisa que eu resolvo.

