Preciso de ajuda no estudo desta função:
f(x)=
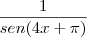
Até agora cheguei a conclusão que:
- Domínio é |R \ {
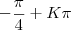}- Contra dominio = ]-?-1] ? [1, +?]
- Não tem zeros. (equaçao deu impossível)
- É ímpar. ( provei que
)- Período é
- Não tem função inversa (pq não é injectiva)
Falta me ver:
Se é ou não continua, se é diferenciavel, ver os intervalos de monotonia, os extremos, o sentido de concavidade, e as assimptotas.
E um exemplo dum problema da 'vida real' para esta função ...
Tenho de provar tudo com cálculos...
Agradeço qualquer correcção/explicação/ajuda em qualquer um destes tópicos, é um bocado urgente ...
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.