Materiais sobre Cálculo.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por salles2000 » Ter Nov 17, 2009 15:57
por salles2000 » Ter Nov 17, 2009 15:57
Olá a todos!
Gostaria de ajuda para montar uma fórmula para calcular a porcentagem reversa, se for este o termo a ser utilizado:
Vou usar um número inteiro para facilitar a explicação, mas preciso aplicar isto em várias situações com valores que incluem centavos e gostaria de saber se é possível voltar no valor original com exatidão ?
Tenho o valor, 108,00 e sei que sobre este valor foi aplicado 8%, como faço para saber qual era o valor original antes de ter sido aplicada a porcentagem ?
Se eu fizer o cálculo direto 108,00 - 8% = 99,36, quando na verdade sabemos que o valor correto seria 100,00, mas quando deduzo 8% de 108,00 estou deduzindo também do percentual já aplicado.
Como calcular para achar o valor original ?
Atenciosmente,
Salles
-
salles2000
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 17, 2009 15:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Lucio Carvalho » Ter Nov 17, 2009 16:56
por Lucio Carvalho » Ter Nov 17, 2009 16:56
Olá salles 2000,
De acordo com o teu problema, sabemos que, com lucro de 8%, um objecto custa R 108,00. Queremos saber, qual é o custo do objecto sem lucro?
Tentarei ajudar, apresentando dois processos.
1º Processo
Seja x o custo do objecto sem lucro.
Então:
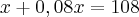
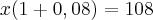
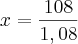

Assim, ficamos a saber que o valor inicial (sem lucro) é de R 100,00
-----------------------------------------------------------------------------------
2º Processo
Tem-se que 108% corresponde a R 108,00.
Então, escrevemos:
108,00 ---------> 108%
x ---------------> 100%
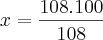

Espero ter ajudado.
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por salles2000 » Qua Nov 25, 2009 14:35
por salles2000 » Qua Nov 25, 2009 14:35
Lucio,
Muito obrigado, sua explicação foi muito útil.
Resolvi a questão dividindo os valores por 1,08 diretamente.
Obrigado.
Att.
Salles
-
salles2000
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 17, 2009 15:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Informática
- Andamento: formado
 por Christian Almeida » Sex Jul 13, 2012 19:25
por Christian Almeida » Sex Jul 13, 2012 19:25
A pergunta é velha, mas gostaria de deixar outra resposta para aqueles que possam interessar.
Se X + P1% = Y e Y - P2% = X,
temos P2=(1- (1 / (1 + P1/100)))*100
Nos valores em questão:
108 - 7.407407407% = 100 , onde 7.407407407% = (1- (1 / (1 + 8/100)))*100
-
Christian Almeida
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Jul 13, 2012 19:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4576 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7904 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3746 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3678 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2916 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


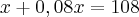
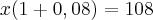
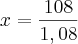

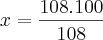



 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
