MAT0134
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por ewald » Sex Abr 13, 2012 00:20
por ewald » Sex Abr 13, 2012 00:20
Ola, tem uma questao no meu livro que nao esta batendo com o gabarito de nenhuma forma. Como o titulo ja diz a questao é de mudança de base e segue abaixo.
7. Considere
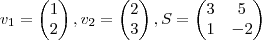
Encontre vetores
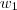
e
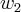
tais que S é a matriz mudança de base de [
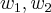
] para [
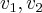
].
Entao, continuando, no livro diz que para achar a matriz de mudança de base contraria, ou seja, que faça o inverso do que "S" faz, precisa-se inverter a matriz "S". Ta falei um pouco enrolado, mas abaixo vou colocar a equaçao:

onde:
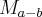
--> Matriz mudança da base "a" p/ "b"

--> Matriz mudança da base "b" p/ "a"
Sendo assim calculei a inversa de "S".

Depois disso calculei os vetores pedidos, fazendo:
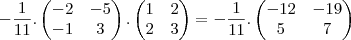
Ou seja, nos meus calculos os vetores ficaram:
w1 =
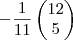
e w2 =

Pronto é isso, se alguem puder por favor corrigir meu erro, eu agradeço imensamente.
-
ewald
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Qui Mai 05, 2011 17:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Eletrica
- Andamento: cursando
Voltar para Introdução à Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Mudança de Base] Matriz de mudança de base ? para ?.
por fabriel » Ter Nov 26, 2013 15:38
- 0 Respostas
- 2108 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:38
Álgebra Linear
-
- Mudança de Base
por Bruhh » Sáb Nov 20, 2010 17:30
- 0 Respostas
- 1365 Exibições
- Última mensagem por Bruhh

Sáb Nov 20, 2010 17:30
Geometria Analítica
-
- MUDANÇA DE BASE
por renatoneumann » Qui Ago 29, 2013 16:58
- 1 Respostas
- 1590 Exibições
- Última mensagem por e8group

Qui Ago 29, 2013 18:46
Logaritmos
-
- Mudança de base
por Thalis » Qui Jul 24, 2014 01:34
- 1 Respostas
- 2497 Exibições
- Última mensagem por Pessoa Estranha

Qui Jul 24, 2014 23:31
Álgebra Linear
-
- logaritmos - mudança de base
por Raquel » Seg Mar 29, 2010 20:02
- 2 Respostas
- 7280 Exibições
- Última mensagem por rodrigorfg

Sáb Abr 10, 2010 01:26
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
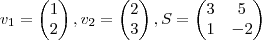
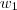 e
e 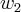 tais que S é a matriz mudança de base de [
tais que S é a matriz mudança de base de [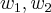 ] para [
] para [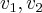 ].
].
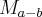 --> Matriz mudança da base "a" p/ "b"
--> Matriz mudança da base "a" p/ "b" --> Matriz mudança da base "b" p/ "a"
--> Matriz mudança da base "b" p/ "a"
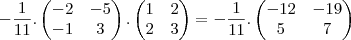
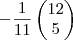 e w2 =
e w2 = 




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.