Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por alexandre32100 » Qui Ago 19, 2010 14:43
por alexandre32100 » Qui Ago 19, 2010 14:43
Eu estava mexendo em minhas coisas quando vi uma imagem, similar a abaixo, onde consta a prova de que

.
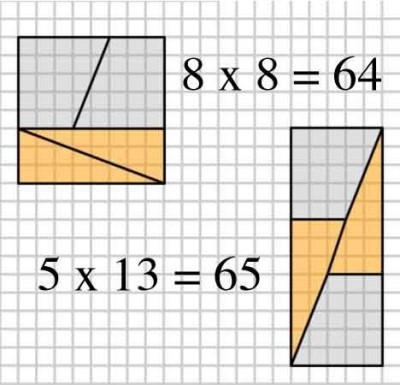
- não há erro, as peças são idênticas nas duas figuras
Entretanto todos nós sabemos que isto está longe de ser verdade, além disso posso afirmar: há uma "trapaça" nesta prova.
Mas onde, qual é a "trapaça"?
-
alexandre32100
-
 por Elcioschin » Qui Ago 19, 2010 17:47
por Elcioschin » Qui Ago 19, 2010 17:47
A 1ª figura é perfeita. A segunda não!
Faça o seguinte:
Desenhe a 1ª figura (um quadrado de 8 cm de lado) e recorte conforme indicado.
Você terá obtido dois triângulos retângulos iguais e dois trapézios retângulos iguais.
O ângulo menor  do triângulo tem inclinação tg = 3/8 ----> tg = 0,375
Pelo vértice obtuso O do trapézio trace uma linha paralela à altura do trapézio. Você terá dividido o trapézio em um retângulo e um triângulo. O ângulo menor Ô deste triângulo tem inclinação tgÔ = 2/5 ----> tgÔ = 0,400
Assim, as duas inclinações são DIFERENTES, embora próximas. Se você juntar as hipotenusas dos dois triângulos, NUNCA obterá uma reta
Tente agora juntar as 4 partes como mostrado na figura 2. Você verá que é impossível.
Para se obter um retângulo conforme a 2ª figura, ficará no meio, na junção entre as hipotenusas dos triângulos, um espaço vazio. A área deste espaço vazio é igual a 1 cm².
Assim, a área DE PAPEL, na 2ª figura vale 5*13 - 1 = 65 - 1 = 64 ----> Exatamente a área da 1ª figura.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por alexandre32100 » Qui Ago 19, 2010 18:04
por alexandre32100 » Qui Ago 19, 2010 18:04
Ah é.

Na segunda figura, a diagonal é um "espaço vazio", mais precisamente um paralelogramo de área 1cm².
-
alexandre32100
-
Voltar para Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.
 .
.
