 por Isa123 » Dom Dez 29, 2013 10:29
por Isa123 » Dom Dez 29, 2013 10:29
Olá, Sou dos Açores em Portugal e estou a realizar um trabalho para entregar, mas estou com dúvidas!
Por favor podem me ajudar?
Os exercicios são esses:



Por favor me ajudem!!

-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 29, 2013 17:05
por e8group » Dom Dez 29, 2013 17:05
Bem vinda ao Fórum .Por favor leia as regras, é permitido uma questão por tópico e além disso anexe imagens somente se for estritamente necessário . Lá vai uma dica p/ a primeira questão ....
O teorema binomial nos garante que
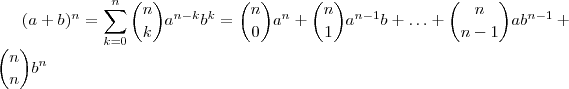
.
(a,b números reais quaisquer e n natural)
Pode-se notar que o i-ésimo termo do desenvolvimento acima é
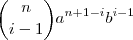
.
Trocando

por
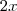
e

por
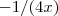
e utilizando a informação dada poderá determinar

.Tente concluir.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Isa123 » Dom Dez 29, 2013 21:07
por Isa123 » Dom Dez 29, 2013 21:07
Peço desculpa desde já! Vou já retificar.
Tenho muitas dificuldades em Matemática e não estou a entender

-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 29, 2013 22:13
por e8group » Dom Dez 29, 2013 22:13
Boa noite . O teorema binomial , aquele mencionado acima será usado agora para desenvolver
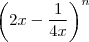
. Se tomarmos
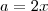
e
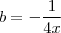
teremos que
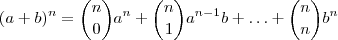
.Em que
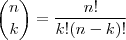
.
De acordo com esta soma verificamos que o segundo termo da esquerda p/ direita é :
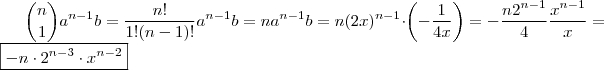
.A expressão destacada deve ser igual aquela dada pelo exercício . Tente concluir.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Isa123 » Seg Dez 30, 2013 10:47
por Isa123 » Seg Dez 30, 2013 10:47
Deve tar me a chamar de burra... mas estou com uma branca e estou confundindo tudo

-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Dez 30, 2013 11:40
por e8group » Seg Dez 30, 2013 11:40
Não se preocupe,pode ser falta de prática . O que temos é
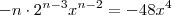
. Uma possível solução natural para

seria a do sistema abaixo
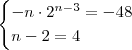
caso o mesmo tenha solução .E ele tem , de fato dá segunda equação temos
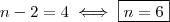
e substituindo isto na primeira eq. ,resulta
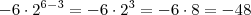
OK! .
OBS.: Dois polinômios são iguais quando todos os coeficientes dos monômios(1,x,x^2,...) de grau correspondente são iguais . O que quero dizer é :
Sendo
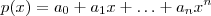
e
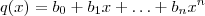
,temos
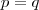
se e somente se
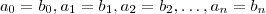
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Isa123 » Seg Dez 30, 2013 20:26
por Isa123 » Seg Dez 30, 2013 20:26
Agora sim entendi!! Estava a fazer uma confusão enorme!
Muitissimo Obrigado!!

Estou adorando aprender consigo poderia-me dar mais umas dicas com os outros exercicios? Se puder claro!

Mais uma vez muito obrigado!!

-
Isa123
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Ter Dez 10, 2013 21:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas
 por Adriana Barbosa » Seg Jun 01, 2009 11:01
por Adriana Barbosa » Seg Jun 01, 2009 11:01
- 1 Respostas
- 1724 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 07:00
Funções
-
- duvidas e + duvidas
por sukita » Ter Out 05, 2010 22:22
- 1 Respostas
- 1675 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 22:31
Progressões
-
- Duvidas
 por Paulo A G » Qua Jan 26, 2011 14:45
por Paulo A G » Qua Jan 26, 2011 14:45
- 1 Respostas
- 3005 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:09
Pedidos de Materiais
-
- 2 dúvidas
por analuiza » Qui Fev 17, 2011 23:14
- 1 Respostas
- 2726 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:33
Trigonometria
-
- Dúvidas ....
por vanessa134 » Seg Out 17, 2011 01:06
- 0 Respostas
- 1512 Exibições
- Última mensagem por vanessa134

Seg Out 17, 2011 01:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










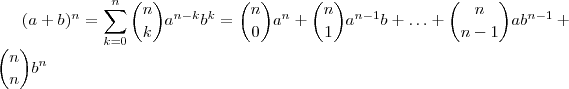 .
. 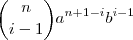 .
. por
por 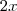 e
e  por
por 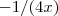 e utilizando a informação dada poderá determinar
e utilizando a informação dada poderá determinar  .Tente concluir.
.Tente concluir.


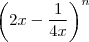 . Se tomarmos
. Se tomarmos 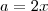 e
e 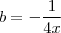 teremos que
teremos que 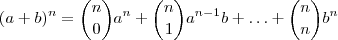 .Em que
.Em que 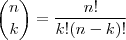 .
.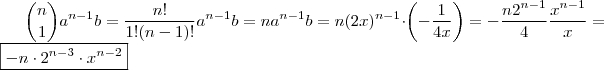 .A expressão destacada deve ser igual aquela dada pelo exercício . Tente concluir.
.A expressão destacada deve ser igual aquela dada pelo exercício . Tente concluir.


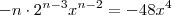 . Uma possível solução natural para
. Uma possível solução natural para  seria a do sistema abaixo
seria a do sistema abaixo 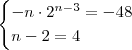 caso o mesmo tenha solução .E ele tem , de fato dá segunda equação temos
caso o mesmo tenha solução .E ele tem , de fato dá segunda equação temos 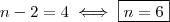 e substituindo isto na primeira eq. ,resulta
e substituindo isto na primeira eq. ,resulta 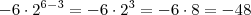 OK! .
OK! . 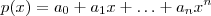 e
e 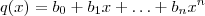 ,temos
,temos 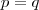 se e somente se
se e somente se 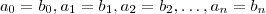 .
.






 , avisa que eu resolvo.
, avisa que eu resolvo.

