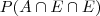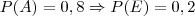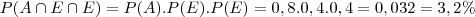por Geriane07 » Qui Ago 08, 2013 13:00
Olá, estou com dúvida na pergunta que citarei a seguir. Eu pensei de várias maneiras, mas creio que de todas as formas erradas, pois não consegui chegar ao resultado final. Para quem me ajudar, desde já obrigada!!!
- Um famoso jogador de basquete do NBB - Novo Basquete Brasil, ao arremessar um lance livre, tem 80% de chances de acertar o arremesso. Num determinado lance do jogo, ao arremessar uma bola da linha dos 3 pontos, recebe uma falta e tem o direito a três arremessos de lance livre. Calcule a probabilidade deste jogador acertar somente o primeiro lance livre.
a) 3,2%
b) 20%
c) 4,7%
d) 80%
e) 14%
Alternativa correta: a) 3,2%
-
Geriane07
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Qui Ago 08, 2013 12:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
por temujin » Qui Ago 08, 2013 17:22
Olá.
Acho que a maneira mais simples é vc construir primeiro o espaço amostral e depois atribuir as probabilidades.
Veja que se ele acerta o primeiro e erra os outros, vc pode descrever o espaço como {A,E,E}, onde A é o evento acerta e E o evento erra. A probabilidade que vc quer, então é:
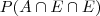
Se a probabilidade de acertar é 80%, então:
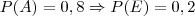
Faz sentido pensar que os arremessos são eventos independentes, ou seja, o resultado de um não interfere na probabilidade dos outros. Logo,
-
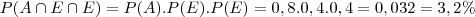
temujin
- Usuário Parceiro
-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
por Geriane07 » Qui Ago 08, 2013 20:41
Obrigada!!! Pude agora compreender o exercício
-
Geriane07
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Qui Ago 08, 2013 12:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
Voltar para Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
