Urgente:Exercício de probabilidade

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Urgente:Exercício de probabilidade

Regras do fórum
Responder

Urgente:Exercício de probabilidade

Mensagempor rudson01 » Qua Mai 22, 2013 00:55

Com os algorismo 1,4,6,8 pode-se formar vários numero de três algorismo distintos.Qual e a soma de todos esse números.

a - 12654
b - 12740
c - 13124
d - 13210
e - 13320


Professor coloco isso pra ajudar :
OBs considerando a sequencia 1,2,3...9,10 de Nº naturais temos que a soma dos 10 numero e dado por

(1+10)*10
tudo divido por 2


legenda

1 = primeiro numero
10 = Ultimo numero
10 = quantidade de numero

Tentei fazer na mão ficou muito grande e o resultado deu errado ai não vou postar.
rudson01
Novo Usuário
Novo Usuário
 
Mensagens: 6
Registrado em: Ter Abr 09, 2013 23:06
Formação Escolar: GRADUAÇÃO
Área/Curso: ANÁLISE E DESENVOLVIMENTO DE SISTEMAS
Andamento: cursando
Voltar ao topo

Re: Urgente:Exercício de probabilidade

Mensagempor Molina » Qui Mai 23, 2013 21:33

Boa noite, Rudson.

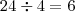Perceba que podemos formar 4 \cdot 3 \cdot 2 = 24 números com estes algarismos distintos. Como há quatro algarismos possíveis, note que 24 \div 4 = 6 é o número que cada algarismo vai aparecer na unidade, da dezena e na centena.

Fazendo o caso da unidade, todos os outros casos são análogos:

Haverá seis algarismos 8 na unidade: 8+8+8+8+8+8 = 48
Haverá seis algarismos 6 na unidade: 6+6+6+6+6+6 = 36
Haverá seis algarismos 4 na unidade: 4+4+4+4+4+4 = 24
Haverá seis algarismos 1 na unidade: 1+1+1+1+1+1 = 6

Logo, a soma de todos os algarismos da unidade será 114.

Analogamente, os algarismos da dezena e da centena serão 114 também. Porem como são dezena e centena, representamos como sendo 1140 e 11400, respectivamente.

Somando: 11400 + 1140 + 114 = 12654


:y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo
Responder

Voltar para Probabilidade

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Princípio da Indução Finita
Autor: Fontelles - Dom Jan 17, 2010 14:42

Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?
2n \geq n+1 ,\forall n \in\aleph*
O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois 2.1 \geq 1+1
2°) Admitamos que P(k), k \in \aleph*, seja verdadeira:
2k \geq k+1 (hipótese da indução)
e provemos que 2(k+1) \geq (K+1)+1
Temos: (Nessa parte)
2(k+1) = 2k+2 \geq (k+1)+2 > (k+1)+1

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Seg Jan 18, 2010 01:55

Boa noite Fontelles.

Não sei se você está familiarizado com o Princípio da Indução Finita, portanto vou tentar explicar aqui.

Ele dá uma equação, no caso:

2n \geq n+1, \forall n \in \aleph^{*}

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

2*1 \geq 1+1

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que k seja verdadeiro, e pretendemos provar que também é verdadeiro para k+1.

\mbox{Suponhamos que P(k), }k \in \aleph^{*},\mbox{ seja verdadeiro:}
2k \geq k+1

\mbox{Vamos provar que:}
2(k+1) \geq (k+1)+1

Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.

Espero ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Fontelles - Seg Jan 18, 2010 02:28

Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!

Assunto: Princípio da Indução Finita
Autor: Fontelles - Qui Jan 21, 2010 11:32

Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Jan 21, 2010 12:25

Boa tarde Fontelles!

Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.

O que temos que provar é isso: 2(k+1) \geq (k+1)+1, certo? O autor começou do primeiro membro:

2(k+1)= 2k+2

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

2k+2 \geq (k+1)+2

Que é outra verdade. Agora, com certeza:

(k+1)+2 > (k+1)+1

Agora, como 2(k+1) é \geq a (k+1)+2, e este por sua vez é sempre > que (k+1)+1, logo:

2(k+1) \geq (k+1)+1 \quad \mbox{(c.q.d)}

Inclusive, nunca é igual, sempre maior.

Espero (dessa vez) ter ajudado.

Um abraço.

Assunto: Princípio da Indução Finita
Autor: Caeros - Dom Out 31, 2010 10:39

Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?

Assunto: Princípio da Indução Finita
Autor: andrefahl - Dom Out 31, 2010 11:37

c.q.d. = como queriamos demonstrar =)

Assunto: Princípio da Indução Finita
Autor: Abelardo - Qui Mai 05, 2011 17:33

Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.

Assunto: Princípio da Indução Finita
Autor: MarceloFantini - Qui Mai 05, 2011 20:05

Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Assunto: Princípio da Indução Finita
Autor: Vennom - Qui Abr 26, 2012 23:04

MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.

Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa. :-D

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum