Dada a equação x + x‚ + ... + xn = k, na qual k N, chama-se solução inteira dessa equação a toda n-pla de números inteiros (?,?‚, ..., ?n), tal que ? + ?‚ + ... + ?n = k. Assim, por exemplo, as ternas (6, 10, 3) e (-2, 9, 12) são soluções inteiras da equação x + y + z = 19. Sabe-se que o número de soluções inteiras e positivas da equação x + x‚ + ... + xn = k é dado pela combinação (C) de k - 1 elementos, n - 1 a n - 1. Nessas condições, se a equação x + y + z = k tem 36 soluções inteiras e positivas, então uma solução dessa equação é:
a) (2, 1, 3)
b) (4, 2, 3)
c) (3, 6, 1)
d) (5, 3, 4)
e) (8, 7, 5)


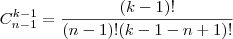
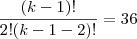
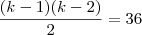
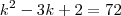




 , avisa que eu resolvo.
, avisa que eu resolvo.

