(G1 - ifsp)

[Maria Livia]

Dispõe-se de cinco cores para colorir o retângulo que está dividido em quatro outros retângulos menores,. R1, R2, R3 e R4, de maneira que retângulos com um lado comum não devem ser coloridos com a mesma cor. O número de modos diferentes de colorir os quatro retângulos com apenas duas cores é

[Rafael16]

Boa noite Maria Livia!

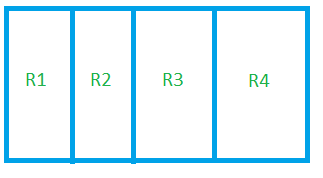
Sem título.png (3.43 KiB) Exibido 14960 vezes

Temos 5 cores.
Em R1 temos então 5 possibilidades. Já em R2 vamos ter só 4, pois em R1 vamos escolher uma cor e vai nos restar 4, já que os retângulos devem ser pintados com duas cores e retângulos de mesmo lado não podem ter a mesma cor.
Em R3 vamos ter 1 possibilidade, que é a cor escolhida em R1, e R4 também vamos ter somente 1 possibilidade, que é a cor escolhida em R2. Ou seja, temos que pintar o retângulo "cor-sim cor-não" somente com duas cores.

R1 = 5 possibilidades
R2 = 4 possibilidades
R3 = 1 possibilidade
R4 = 1 possibilidade

R1 * R2 * R3 * R4 = 20

Espero ter ajudado!

[Maria Livia]

obg!

[anaflaviasouza]

Dispõe-se de cinco cores para colorir o retângulo que está dividido em quatro outros retângulos menores,. R1, R2, R3 e R4, de maneira que retângulos com um lado comum não devem ser coloridos com a mesma cor. O número de modos diferentes de colorir os quatro retângulos com apenas duas coresé?

tive um pouco de dificuldade em entender a resolução apresentada aqui, porque utilizar as 5 cores se no final do exercício ele deixou definido que os quatro retângulos fossem pintados com apenas duas cores?

[anaflaviasouza]

Dispõe-se de cinco cores para colorir o retângulo que está dividido em quatro outros retângulos menores,. R1, R2, R3 e R4, de maneira que retângulos com um lado comum não devem ser coloridos com a mesma cor. O número de modos diferentes de colorir os quatro retângulos com apenas duas coresé?

tive um pouco de dificuldade em entender a resolução apresentada aqui, porque utilizar as 5 cores se no final do exercício ele deixou definido que os quatro retângulos fossem pintados com apenas duas cores?