
Então, resolvendo esse exercício , melhor dizendo, TENTANDO resolver, acabei não conseguindo e parti em busca do gabarito, que também está no anexo do exercício. A questão é, não concordei com a resolução, pois não sei se realmente está "errado" ou se eu -mais uma vez- me confundi na teoria. Por exemplo, quando o exercício "diz" que VI. 640 filiados votaram a favor de C, mas não de A ou de B, ele coloca os 640 todinho no C, e eu aprendi que esse valor não é somente os filiados que votaram em C, e sim está incluso os outros 2 (A e B). Do mesmo modo que em B. Segue outro anexo com o meu raciocínio. Nele, eu fiz à primeira vista, fiz também as hachuras de cada item, pois esse seria o meu outro raciocínio que vai de acordo com o gabarito, se eu realmente colocasse os respectivos valores em cada mancha. Resumindo meus dois raciocínios: 1° pensei que os valores dados não eram exclusivos para cada conjunto, e assim desenvolvi como segue no anexo. Já na 2° pensei baseado nas hachuras que fiz, e assim daria certo. Mas quero saber o porquê do 1° raciocínio não dar certo.
Conto com a paciência e a genialidade de vocês, que sem dúvidas são quase inevitáveis
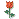



 ; ou seja, SOMENTE os que votaram em C...
; ou seja, SOMENTE os que votaram em C...
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.