O conjunto
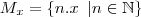
representa o conjunto de todos os múltiplos inteiros do número

. Se
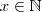
então este conjunto é, vulgarmente, a "tabuada" de x.
Daí,
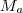
é o conjunto de todos os múltiplos inteiros de

e
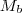
o conjunto de todos os múltiplos inteiros de

.
Assim, para que
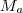
seja subconjunto de
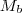
é preciso que
todos os elementos de
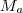
sejam "encontrados" em
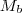
.
Ou seja, para qualquer elementos
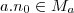
é necessário que exista um
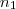
tal que
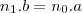 para todo
para todo 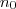
.
Logo, como b deve ser natural, é preciso que b seja tal que
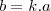
com k natural, já que, daí,
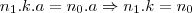
.
Portanto,

deve ser divisor de

.
Por exemplo, escolha

e

.
Daí,
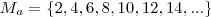
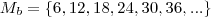
Note que , nesse caso,
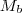
é subconjunto de
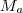
pois

divide

. Para a situação contrária, que é o caso da questão, é o contrário:

divide

.
 Naturais} e Mb = {n. b | n
Naturais} e Mb = {n. b | n  Naturais}, com a e b naturais não nulos, então Ma é subconjunto de Mb sempre que:
Naturais}, com a e b naturais não nulos, então Ma é subconjunto de Mb sempre que:

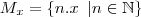 representa o conjunto de todos os múltiplos inteiros do número
representa o conjunto de todos os múltiplos inteiros do número  . Se
. Se 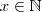 então este conjunto é, vulgarmente, a "tabuada" de x.
então este conjunto é, vulgarmente, a "tabuada" de x.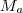 é o conjunto de todos os múltiplos inteiros de
é o conjunto de todos os múltiplos inteiros de  e
e 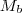 o conjunto de todos os múltiplos inteiros de
o conjunto de todos os múltiplos inteiros de  .
.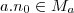 é necessário que exista um
é necessário que exista um 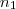 tal que
tal que 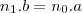
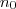 .
.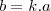 com k natural, já que, daí,
com k natural, já que, daí, 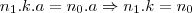 .
. e
e  .
.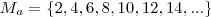
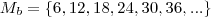

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.