ifba

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

ifba

Regras do fórum
Responder

ifba

Mensagempor zenildo » Ter Set 24, 2013 15:07

O CAIXA DE UM BANCO TROCOU A ORDEM DE DOIS ALGARISMOS DE VALOR DA CONTA A SER PAGA POR UM CLIENTE, COBRANDO R$ 27,00 A MAIS.SENDO 11 A SOMA DOS ALGARISMOS, O VALOR CORRETO A SER PAGO PELO CLIENTE ERA DE:

A) R$ 29,00
B) R$ 38,00
C) RS 47,00
D) R$ 74,00
E) RS 83,00
zenildo
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 309
Registrado em: Sáb Abr 06, 2013 20:12
Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
Formação Escolar: EJA
Área/Curso: PRETENDO/ DIREITO
Andamento: cursando
Voltar ao topo

Re: ifba

Mensagempor DanielFerreira » Qui Fev 20, 2014 18:22

Zenildo,
poderíamos chegar a resposta "trabalhando"as alternativas!

zenildo escreveu:O CAIXA DE UM BANCO TROCOU A ORDEM DE DOIS ALGARISMOS DE VALOR DA CONTA A SER PAGA POR UM CLIENTE, COBRANDO R$ 27,00 A MAIS.SENDO 11 A SOMA DOS ALGARISMOS, O VALOR CORRETO A SER PAGO PELO CLIENTE ERA DE:

A) R$ 29,00
B) R$ 38,00
C) RS 47,00
D) R$ 74,00
E) RS 83,00


Consideremos que o valor a ser pago seja: XY

Segundo o enunciado,

XY
+
27
===
YX

Uma vez que, Y > X; ao somar (Y + 7) "vai" UM em cima do X!

Daí,

\\ (1 + x) + 2 = y \\ x = y - 3


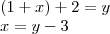
Sabemos que,

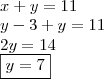
\\ x + y = 11 \\ y - 3 + y = 11 \\ 2y = 14 \\ \boxed{y = 7}

E,

\\ x = y - 3 \\ x = 7 - 3 \\ \boxed{x = 4}
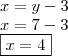
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
DanielFerreira
Colaborador - em formação
Colaborador - em formação
 
Mensagens: 1732
Registrado em: Qui Jul 23, 2009 21:34
Localização: Mangaratiba - RJ
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - IFRJ
Andamento: formado
Voltar ao topo
Responder

Voltar para Conjuntos

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

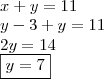
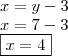
Índice do fórum