A sua estratégia está correta. Você tem que expressar os conjuntos

,

e

com os seus respectivos elementos explicitamente para visualizar melhor as intersecções e uniões.
Os elementos do conjunto

são todos aqueles do conjunto
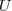
que menores que 0. Ou seja, todos os elementos negativos de
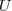
. Assim, verificando, temos
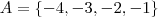
.
Os elementos do conjunto

são todos aqueles do conjunto
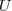
que são menores que 2 e maiores que 3 . Assim, verificando, temos
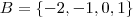
. Note aqui que a notação
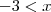
e
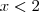
significa que temos de selecionar todos os elementos de
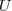
que se incluem nesse intervalo mas EXCLUINDO o próprio -3 e 2. Do contrário seria
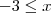
e
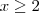
. Entende porque? Veja a definição de intervalo aberto e fechado.
Os elementos do conjunto

, finalmente, são todos aqueles do conjunto
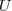
que são maiores OU IGUAL a -1 . Assim, verificando, temos
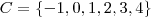
. Aqui, inclui-se o próprio -1.
A operação "intersecção" entre dois conjuntos gera um novo conjunto cujos elementos são a captura de todos os elementos comuns a eles. Por exemplo,
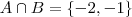
pois são os únicos elementos que pertencem a

e

simultaneamente .
Já a operação "união" entre dois conjuntos gera um novo conjunto cujos elementos são a junção(ou união, como o nome mesmo já diz) de todos os elementos desses conjuntos. Nota: se um elemento pertence ao dois conjuntos simultaneamente, isto é, se este elemento pertence a intersecção dos conjuntos, ele deve ser acrescentado a união dos mesmos uma única vez. Por exemplo,
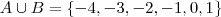
Os elementos -2 e -1 pertencem a intersecção de

e

(como calculamos no 1° exemplo) e apareceram uma única vez no conjunto união.
Tente prosseguir.
 U|x<0}, B = {x
U|x<0}, B = {x U|-3<x<2} e C = {X
U|-3<x<2} e C = {X U|x
U|x -1} Determine:
-1} Determine: B
B  C
C B
B  C
C (B
(B A)
A) A)
A)  C
C )
)

 ,
,  e
e  com os seus respectivos elementos explicitamente para visualizar melhor as intersecções e uniões.
com os seus respectivos elementos explicitamente para visualizar melhor as intersecções e uniões.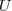 que menores que 0. Ou seja, todos os elementos negativos de
que menores que 0. Ou seja, todos os elementos negativos de 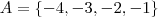 .
. 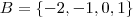 . Note aqui que a notação
. Note aqui que a notação 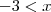 e
e 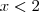 significa que temos de selecionar todos os elementos de
significa que temos de selecionar todos os elementos de 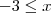 e
e 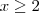 . Entende porque? Veja a definição de intervalo aberto e fechado.
. Entende porque? Veja a definição de intervalo aberto e fechado.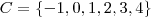 . Aqui, inclui-se o próprio -1.
. Aqui, inclui-se o próprio -1.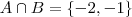
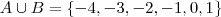

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.