Poderiam me ajudar a resolver os seguintes exercicios deconjunto:
1) 52 pessoas discutem a preferência por dois produtos A e B, entre outros e conclui-se que o número de pessoas que gostavam de B era:
I - O quádruplo do número de pessoas que gostavam de A e B;
II - O dobro do número de pessoas que gostavam de A;
III - A metade do número de pessoas que não gostavam de A nem de B.
Nestas condições, o número de pessoas que não gostavam dos dois produtos é igual a:
a) 48 b) 35 c) 36 d) 47 e) 37
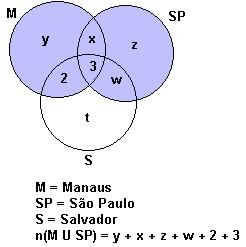
2) 35 estudantes estrangeiros vieram ao Brasil. 16 visitaram Manaus; 16, S. Paulo e 11, Salvador. Desses estudantes, 5 visitaram Manaus e Salvador e, desses 5, 3 visitaram também São Paulo. O número de estudantes que visitaram Manaus ou São Paulo foi:
a) 29 b) 24 c) 11 d) 8 e) 5




 .
.
 :
: