Estou com uma dúvida na interpretação da questão abaixo... Gostaria que me ajudasse por favor!
A questão é a seguinte ---> Determine o produto cartesiano do cojunto
![]1,3] X [3,5[ ]1,3] X [3,5[](/latexrender/pictures/3846e65b4e4ed972832628f8e7837049.png) e sua forma gráfica.
e sua forma gráfica.Bom... Quanto ao produto acho que seria isso--> {(1,3),(1,5),(3,3),(3,5)}
Quanto a foma gráfica estou com dúvida!!! O primeiro produto, por exemplo --> ( 1 está em aberto, 3 está fechado ), na hora de montar a forma gráfica, o ponto ( par ordenado (1,3), seria aberto ou fechado? ) ????
Se tiver como esquematizar o probelema pelo editor de fórmulas seria grato.
Ajude-me por favor.
Forte abraço.
Até mais.



![]1, 3] = \left\{ 2, 3 \right\} ]1, 3] = \left\{ 2, 3 \right\}](/latexrender/pictures/54669fd374487d6f1171ddd7cba090f6.png)
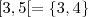
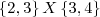
![[1, 5] = \left\{ 1, 2, 3, 4, 5 \right\} [1, 5] = \left\{ 1, 2, 3, 4, 5 \right\}](/latexrender/pictures/0bddefb5df63a88a76505b025e6ac656.png)
![]1, 5[ = \left\{2, 3, 4 \right\} ]1, 5[ = \left\{2, 3, 4 \right\}](/latexrender/pictures/7f8830c6811c0fbefc346001f20e933d.png)
![]1, 5] = \left\{2, 3, 4, 5 \right\} ]1, 5] = \left\{2, 3, 4, 5 \right\}](/latexrender/pictures/d59cf06260a8fe2e4cbea3674f87fb2d.png)
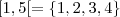
![[-2, 1] = \left\{-2, -1, 0, 1 \right\} [-2, 1] = \left\{-2, -1, 0, 1 \right\}](/latexrender/pictures/397d9c6c0a3bed41784b917e4fd04f17.png)
![]-2, 1] = \left\{-1, 0, 1 \right\} ]-2, 1] = \left\{-1, 0, 1 \right\}](/latexrender/pictures/226cf59f9e8e15563a86bc1dd245fcaf.png)
![]-2, 1[ = \left\{-1, 0 \right\} ]-2, 1[ = \left\{-1, 0 \right\}](/latexrender/pictures/c06305d50407fccc5bf3ca8964249e48.png)
![]1, 3[ = \left\{ 2 \right\} ]1, 3[ = \left\{ 2 \right\}](/latexrender/pictures/832b7f5c36ee31b9f08deb68f5bfc926.png)


 .
.
 :
: