 por lais1906 » Qui Out 11, 2012 14:58
por lais1906 » Qui Out 11, 2012 14:58
sabendo que a fração

é equivalente a

e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b

=

2.a-b=4
consegui montar mais não sei resolver me ajudem
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por MarceloFantini » Qui Out 11, 2012 15:14
por MarceloFantini » Qui Out 11, 2012 15:14
Se

, então

. Da segunda equação, se

então

, logo

. Termine.
Editado pela última vez por
MarceloFantini em Qui Out 11, 2012 15:52, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Qui Out 11, 2012 15:20
por Cleyson007 » Qui Out 11, 2012 15:20
Olá, boa tarde!
Parabéns! Montou corretamente, agora é só resolver..
O Fantini cometeu um pequeno erro em
5b = 3a.
Da primeira equação, temos:

Multiplicando cruzado, temos:

Logo, temos um sistema de equações com duas incógnitas (a e b). Basta resolver.. Vou fazer por "substituição", acompanhe:

Substitua o valor de "a" na segunda equação.
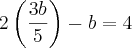
Consegue seguir a partir daqui?
Qualquer coisa estou por aqui

Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Qui Out 11, 2012 15:51
por MarceloFantini » Qui Out 11, 2012 15:51
Obrigado pela correção.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lais1906 » Sáb Out 13, 2012 00:44
por lais1906 » Sáb Out 13, 2012 00:44
esta correto ?

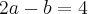
multiplicando em x fica

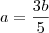
subistituindo vai ficar
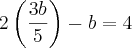
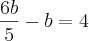
fazendo o mmc fica
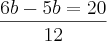
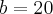
então
2a-b=4
2a-20=4
2a=20+4
2a=24
a=
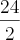
a=12
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por MarceloFantini » Sáb Out 13, 2012 00:53
por MarceloFantini » Sáb Out 13, 2012 00:53
Não precisa fazer MMC, multiplique tudo por 5. A partir disso refaça as contas, pois você errou deste ponto em diante.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lais1906 » Sáb Out 13, 2012 01:08
por lais1906 » Sáb Out 13, 2012 01:08
você fala para mim multipicar
6b-b=4 (5)
30b-5b=20 isso?
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
 por MarceloFantini » Sáb Out 13, 2012 01:15
por MarceloFantini » Sáb Out 13, 2012 01:15
Quase. O correto é

, daí

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Dom Out 14, 2012 14:15
por DanielFerreira » Dom Out 14, 2012 14:15
Lais1906,
mais uma forma de resolver:
Condição I: Condição II:
Condição II:
Substituindo
I em
II, temos:

Para encontrar o valor de

e

substitua

por 4, isto é:

Portanto,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por lais1906 » Sáb Out 20, 2012 03:25
por lais1906 » Sáb Out 20, 2012 03:25
obrigada a todos pela ajuda =]
-
lais1906
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Out 11, 2012 14:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciencias contabeis
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3812 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1695 Exibições
- Última mensagem por MarceloFantini

Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4522 Exibições
- Última mensagem por Claudin

Seg Jun 06, 2011 18:34
Matemática Financeira
-
- Fração 110
por Raphael Feitas10 » Seg Jan 09, 2012 17:28
- 1 Respostas
- 1855 Exibições
- Última mensagem por Arkanus Darondra

Seg Jan 09, 2012 18:43
Sistemas de Equações
-
- Fração 112
por Raphael Feitas10 » Sex Jan 13, 2012 02:23
- 1 Respostas
- 1673 Exibições
- Última mensagem por ant_dii

Sex Jan 13, 2012 03:18
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é equivalente a
é equivalente a  e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b
e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b =
=

 é equivalente a
é equivalente a  e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b
e que o dobro do numerador menos o denominador é igual a 4 calcule o valor de a.b =
=

 , então
, então  . Da segunda equação, se
. Da segunda equação, se  então
então  , logo
, logo  . Termine.
. Termine.




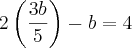




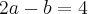

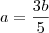
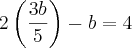
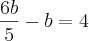
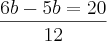
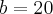
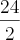








 e
e  substitua
substitua  por 4, isto é:
por 4, isto é:


