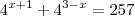
Tentei resolver da seguinte maneira:
Chamei
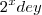 e fatorei o 4 e fiz as substituições, aí ficou:
e fatorei o 4 e fiz as substituições, aí ficou: 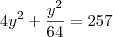
eu encontrei como restultado y = 8, y =-8 como
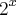 > 0 então y = 8. fazendo
> 0 então y = 8. fazendo 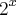 = 8 eu encontro x = 3. Mas segundo a resposta do livro, a resposta é 3 e -1. Não consigo encontrar -1 como resposta, esse é o problema...
= 8 eu encontro x = 3. Mas segundo a resposta do livro, a resposta é 3 e -1. Não consigo encontrar -1 como resposta, esse é o problema...


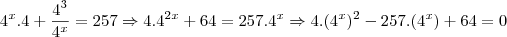 .
. . Aqui esté seu erro: você esqueceu que
. Aqui esté seu erro: você esqueceu que  e não simplismente
e não simplismente 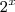 .
.
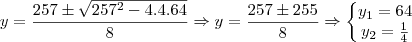
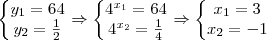

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)