 por +Danilo2 » Sáb Out 08, 2016 18:11
por +Danilo2 » Sáb Out 08, 2016 18:11
Questão. Encontre as possíveis soluções da equação do terceiro grau.
![x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0 x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0](/latexrender/pictures/7d01b86c7fd21a6d329ef05662f9363b.png)
Ao resolver esta equação, cheguei a esse resultado abaixo.
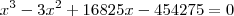
Assim estive pensando em substituir o valor de x por 27, pois esse numero anula esses números maiores, mas não anula o valor de
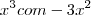
.
Como faço para encontrar a primeira solução?
-
+Danilo2
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Set 29, 2016 10:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por petras » Seg Dez 12, 2016 11:17
por petras » Seg Dez 12, 2016 11:17
Sua resolução está errada. O correto seria
![{x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0 {x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0](/latexrender/pictures/d2c5d5038bb9e65ec0d42d3fa5b9f84a.png)
Por análise percebemos que 1 é raiz então podemos baixar um grau da equação:
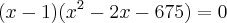
Achando as raízes da funçaõ quadrática teremos x = -25 e x=27
Portanto S={-25,1,27}
-
petras
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Sex Jan 22, 2016 21:19
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Raizes de uma equação de terceiro grau.
por 380625 » Dom Mar 27, 2011 13:58
- 3 Respostas
- 3016 Exibições
- Última mensagem por MarceloFantini

Dom Mar 27, 2011 18:09
Funções
-
- Resolvendo equacção do terceiro grau
por jptuga » Sáb Set 17, 2011 06:02
- 2 Respostas
- 1651 Exibições
- Última mensagem por jptuga

Dom Set 18, 2011 08:58
Polinômios
-
- Arcos no Terceiro Quadrante
por Rafael16 » Sáb Mai 18, 2013 22:53
- 0 Respostas
- 948 Exibições
- Última mensagem por Rafael16

Sáb Mai 18, 2013 22:53
Trigonometria
-
- [Descobrir o terceiro ângulo do triângulo]
por Mayra Luna » Sex Dez 07, 2012 16:25
- 2 Respostas
- 1703 Exibições
- Última mensagem por Mayra Luna

Ter Dez 11, 2012 01:26
Trigonometria
-
- Calcular um terceiro lado do triângulo com apenas dois lados
por Sohrab » Dom Jun 15, 2014 02:55
- 1 Respostas
- 1822 Exibições
- Última mensagem por e8group

Dom Jun 15, 2014 13:18
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0 x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0](/latexrender/pictures/7d01b86c7fd21a6d329ef05662f9363b.png)
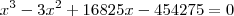
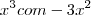 .
.
![x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0 x^3-3x^2 + [27(2-27) +2]x-27(-25)= 0](/latexrender/pictures/7d01b86c7fd21a6d329ef05662f9363b.png)
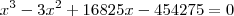
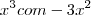 .
.
![{x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0 {x}^{3}-3{x}^{2}+\left[(27.-25)+2) \right]x-27(-25) = 0\\
{x}^{3}-3{x}^{2}-673x+675= 0](/latexrender/pictures/d2c5d5038bb9e65ec0d42d3fa5b9f84a.png)
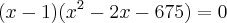

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
