 por brunoguim05 » Qua Mai 28, 2014 15:20
por brunoguim05 » Qua Mai 28, 2014 15:20
Boa tarde pessoal!
Não estou conseguindo desenvolver este exercício e preciso de ajuda ;s
Encontre a equação da circunferência com centro (-2 , 2) e que é tangente a reta com equação 2x-y+1=0
-
brunoguim05
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 28, 2014 15:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduaçao em Agronomia
- Andamento: cursando
 por jcmatematica » Sex Set 26, 2014 10:15
por jcmatematica » Sex Set 26, 2014 10:15
brunoguim05 escreveu:Boa tarde pessoal!
Não estou conseguindo desenvolver este exercício e preciso de ajuda ;s
Encontre a equação da circunferência com centro (-2 , 2) e que é tangente a reta com equação 2x-y+1=0
Calculando a distancia entre o ponto (centro da circunferencia) ate a reta.
![D = \frac{\left|ax+by+c \right|}{\sqrt[2]{{a}^{2}+{b}^{2}}} D = \frac{\left|ax+by+c \right|}{\sqrt[2]{{a}^{2}+{b}^{2}}}](/latexrender/pictures/f39f9984cfa73a93a9aca88d787fb168.png)
![D = \frac{\left|2-1+1 \right|}{\sqrt[2]{{4}+{4}}} D = \frac{\left|2-1+1 \right|}{\sqrt[2]{{4}+{4}}}](/latexrender/pictures/bcd0c40a709b5449a0bcc49b435e9220.png)
![D = \frac{2}{\sqrt[2]{8}} D = \frac{2}{\sqrt[2]{8}}](/latexrender/pictures/da9cc2efe1e9b36ab6ff9b734ae77500.png)
![D = \frac{2.\sqrt[]{8}}{8} D = \frac{2.\sqrt[]{8}}{8}](/latexrender/pictures/3eb521c48bc11a7075df0b1821c7cf9b.png)
![D = \frac{2.2.\sqrt[]{2}}{8} D = \frac{2.2.\sqrt[]{2}}{8}](/latexrender/pictures/38db44e3968de24a384d3e5dde5fe34c.png)
![D = \frac{\sqrt[]{2}}{2} D = \frac{\sqrt[]{2}}{2}](/latexrender/pictures/8cc10119f821010f73da13caab265180.png)
Se a reta e tangente a circunferencia, sabemos que
D e igual ao raio.
Logo, a equacao da circunferencia sera
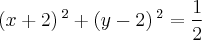
Espero ter ajudado.
-
jcmatematica
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Ter Jul 29, 2014 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação da Circunferência
por Cleyson007 » Qui Abr 08, 2010 15:35
- 1 Respostas
- 11153 Exibições
- Última mensagem por davi_11

Dom Abr 11, 2010 13:46
Geometria Analítica
-
- Equação da circunferência
por PedroSantos » Dom Jan 09, 2011 16:38
- 3 Respostas
- 2210 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 12:18
Geometria Plana
-
- Equação da circunferência
por Andreza » Sáb Fev 25, 2012 09:43
- 1 Respostas
- 1514 Exibições
- Última mensagem por Guill

Sáb Fev 25, 2012 11:43
Geometria Analítica
-
- Equação na Circunferência
por Fernandobertolaccini » Dom Mai 11, 2014 14:48
- 1 Respostas
- 1247 Exibições
- Última mensagem por jcmatematica

Sex Set 26, 2014 10:26
Geometria Analítica
-
- Equação da circunferência
por YuriFreire » Seg Ago 25, 2014 23:22
- 2 Respostas
- 1378 Exibições
- Última mensagem por YuriFreire

Ter Ago 26, 2014 22:30
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![D = \frac{\left|ax+by+c \right|}{\sqrt[2]{{a}^{2}+{b}^{2}}} D = \frac{\left|ax+by+c \right|}{\sqrt[2]{{a}^{2}+{b}^{2}}}](/latexrender/pictures/f39f9984cfa73a93a9aca88d787fb168.png)
![D = \frac{\left|2-1+1 \right|}{\sqrt[2]{{4}+{4}}} D = \frac{\left|2-1+1 \right|}{\sqrt[2]{{4}+{4}}}](/latexrender/pictures/bcd0c40a709b5449a0bcc49b435e9220.png)
![D = \frac{2}{\sqrt[2]{8}} D = \frac{2}{\sqrt[2]{8}}](/latexrender/pictures/da9cc2efe1e9b36ab6ff9b734ae77500.png)
![D = \frac{2.\sqrt[]{8}}{8} D = \frac{2.\sqrt[]{8}}{8}](/latexrender/pictures/3eb521c48bc11a7075df0b1821c7cf9b.png)
![D = \frac{2.2.\sqrt[]{2}}{8} D = \frac{2.2.\sqrt[]{2}}{8}](/latexrender/pictures/38db44e3968de24a384d3e5dde5fe34c.png)
![D = \frac{\sqrt[]{2}}{2} D = \frac{\sqrt[]{2}}{2}](/latexrender/pictures/8cc10119f821010f73da13caab265180.png)
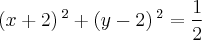


 .
.
 :
: