 por Thiago 86 » Seg Mai 27, 2013 16:58
por Thiago 86 » Seg Mai 27, 2013 16:58
saudações gostaria que alguém me ajuda-se a responder essa equação do 2°grau: o valor de k para que uma das raízes da equação
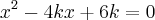
seja o triplo da outra.
Eu tentei fazer assim:
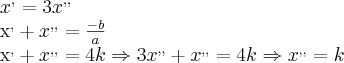
Mas não consigo sair daí.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Cleyson007 » Seg Mai 27, 2013 17:08
por Cleyson007 » Seg Mai 27, 2013 17:08
Boa tarde Thiago!
Siga os passos adotados na resolução que lhe apresento:
http://br.answers.yahoo.com/question/in ... 629AAv0OFrTente aplicar o raciocínio no exercício que você propôs.
Att,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Achar valor de b
por Carolziiinhaaah » Qui Ago 05, 2010 12:32
- 1 Respostas
- 1352 Exibições
- Última mensagem por MarceloFantini

Qui Ago 05, 2010 13:48
Funções
-
- Achar valor de f(-3)
por Carolziiinhaaah » Qui Ago 12, 2010 11:29
- 5 Respostas
- 12895 Exibições
- Última mensagem por Carolziiinhaaah

Sex Ago 13, 2010 17:08
Funções
-
- Achar o valor de R
 por rafaleans » Qua Mar 12, 2014 23:25
por rafaleans » Qua Mar 12, 2014 23:25
- 2 Respostas
- 1815 Exibições
- Última mensagem por rafaleans

Qui Mar 13, 2014 14:47
Inequações
-
- Achar valor do juros.
por laffsj » Ter Dez 29, 2009 19:46
- 0 Respostas
- 1314 Exibições
- Última mensagem por laffsj

Ter Dez 29, 2009 19:46
Matemática Financeira
-
- Inequação - Achar o valor de M
 por rafaleans » Sex Mar 14, 2014 09:21
por rafaleans » Sex Mar 14, 2014 09:21
- 0 Respostas
- 1099 Exibições
- Última mensagem por rafaleans

Sex Mar 14, 2014 09:21
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
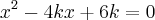 seja o triplo da outra.
seja o triplo da outra.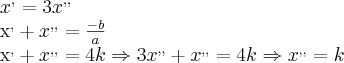

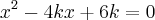 seja o triplo da outra.
seja o triplo da outra.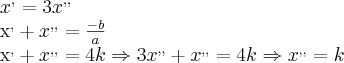



 .
.
 :
: