 por Debylow » Ter Dez 04, 2012 17:07
por Debylow » Ter Dez 04, 2012 17:07
como resolvo ?
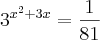
cheguei até aqui , nao sei se esta certo: nao consegui resolver por bhaskara
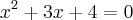
-
Debylow
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Nov 13, 2012 17:37
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Russman » Ter Dez 04, 2012 19:20
por Russman » Ter Dez 04, 2012 19:20
A equação é:
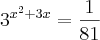
.
Nessas equações exponenciais a técnica é igualar as bases, visto que assim os expoentes devem coincidir. Ou seja, se

então

.
Assim, como
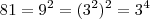
então
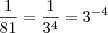
. Portanto,
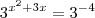
e assim
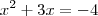
de forma que
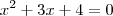
. Resolvendo via Bháskara você deve encontrar duas raízes complexas.
A equação inicial não tem solução Real! Não existe nenhum número Real

que satisfaça
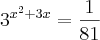
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [equação] Equação exponencial
por kyane » Seg Out 01, 2012 20:30
- 1 Respostas
- 910 Exibições
- Última mensagem por young_jedi

Seg Out 01, 2012 22:13
Equações
-
- Equação exponencial???
por azheng » Sáb Nov 21, 2009 19:47
- 0 Respostas
- 1624 Exibições
- Última mensagem por azheng

Sáb Nov 21, 2009 19:47
Álgebra Elementar
-
- Equação Exponencial
por Adriana Baldussi » Seg Nov 23, 2009 14:41
- 3 Respostas
- 2836 Exibições
- Última mensagem por Molina

Seg Nov 23, 2009 17:07
Álgebra Elementar
-
- Equação Exponencial
por LeonardoSantos » Ter Fev 16, 2010 14:11
- 1 Respostas
- 2826 Exibições
- Última mensagem por Douglasm

Ter Fev 16, 2010 15:46
Funções
-
- Equação exponencial
por cristina » Sex Jun 04, 2010 20:19
- 1 Respostas
- 2239 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 00:27
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
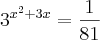
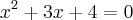

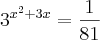
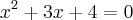

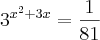 .
. então
então  .
.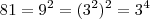 então
então 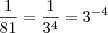 . Portanto,
. Portanto, 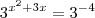
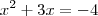 de forma que
de forma que 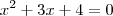 . Resolvendo via Bháskara você deve encontrar duas raízes complexas.
. Resolvendo via Bháskara você deve encontrar duas raízes complexas.  que satisfaça
que satisfaça 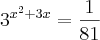 .
.

 .
.
 :
: