brunnkpol escreveu:Obrigado pela sugestão. Usando o método de newton, achei o valor, mas apenas o positivo. O gráfico (pelo programa de computador) mostra que as funções se interceptam no mesmo valor tanto negativo quanto positivo de x
Perfeito !Se pelo metodo de Newton encontrasse ,digamos
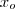
, um valor aproximado para a raiz positiva da eq. dada , ent'ao
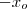
eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.
Desculpe estou com problemas no teclado .
brunnkpol escreveu:Outra dúvida é se existe algum meio que eu possa descobrir simplesmente em quantos pontos uma função intercepta a outra.
Nao sei se ha um metodo especifico . Talvez o TVI ajude . Por exemplo , dadas as funcoes f e g reais , defina h = f-g . Se a funcao h e continua em um intervalo da forma [a,b] e h(a)h(b) < 0 entao pelo TVI existe pelo menos um um numero c entre a e b tal que h(c) = 0 .Mas isto nao nos garanti a quantidade de c presente neste intervalo ,podemos entao reduzir o intervalo usando a metodo da bissecao e verificar se a imagem da funcao oscila o sinal no novo subintervalo e assim por diante .
Tambem podemos verificar se a derivada da funcao eh positiva ou negativa no intrevalo [a,b] , se isto ocorrer juntamente com h(a)h(b) < 0, entao a funcao h possui apenas uma raiz neste intervalo .
Nao sei se estou abilitado para ajudar , mencionei um pouco sobre analise numerica , mas ainda nao estudei tal .Talvez outro membro possa contribuir .
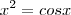


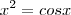



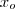 , um valor aproximado para a raiz positiva da eq. dada , ent'ao
, um valor aproximado para a raiz positiva da eq. dada , ent'ao 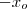 eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.
eh uma aproximacao para a raiz negativa da eq . Isto ocorre pq a funcao cosseno e a definida por x(ao quadrado) sao pares.


 , avisa que eu resolvo.
, avisa que eu resolvo.

