 por Vennom » Qua Set 18, 2013 16:15
por Vennom » Qua Set 18, 2013 16:15
Senhores, por gentileza me ajudem com isso aqui:
(USP) Simplifique:
![\sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}}](/latexrender/pictures/1cec2a67a0cfed29fa364d9b4a198997.png)
Fazendo eu cheguei a isso:
![\sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}} \sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}}](/latexrender/pictures/23b21317c50f3e70e5ab9df2a471c2a4.png)
=>
=
![\sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})}](/latexrender/pictures/d633042033fe640219efd61c667d9c49.png)
=>
=
![\sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})}](/latexrender/pictures/da88b4ba4d376d828a6756b1bcef00b6.png)
=>
=
![\sqrt[2]{63+27\sqrt[2]{3}} \sqrt[2]{63+27\sqrt[2]{3}}](/latexrender/pictures/b7a017c5ada2ba3e612a65df155868a7.png)
=>
Enquanto o gabarito que me foi dado diz que o resultado seria:
![3\sqrt[2]{5+\sqrt[2]{3}} 3\sqrt[2]{5+\sqrt[2]{3}}](/latexrender/pictures/5f5e7b6389df69bbadb03ae53a86535d.png)
=>
![\sqrt[2]{45+9\sqrt[2]{3}} \sqrt[2]{45+9\sqrt[2]{3}}](/latexrender/pictures/3604ee945cbe7386099ab0698c90c716.png)
Vocês podem me dizer onde raios foi que eu errei? Obrigado.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pessoa Estranha » Qua Set 18, 2013 20:36
por Pessoa Estranha » Qua Set 18, 2013 20:36
Olá. Você cometeu um pequeno erro de sinal. Observe o seguinte:
![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)](/latexrender/pictures/e89eab6fc99912f4a593ad52552b441e.png)
Pense como uma "diferença entre dois números elevados ao quadrado".
Tente fazer.... Eu realmente acredito que o erro esteja neste ponto, mas posso estar errada.
Até mais....

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Vennom » Qua Set 18, 2013 20:44
por Vennom » Qua Set 18, 2013 20:44
Pessoa Estranha escreveu:Olá. Você cometeu um pequeno erro de sinal. Observe o seguinte:
![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)](/latexrender/pictures/e89eab6fc99912f4a593ad52552b441e.png)
A regra ai não diz que é igual ao quadrado do primeiro vezes o quadrado do segundo?
Resultando no seguinte:
![(9-3+\sqrt[2]{3}) (9-3+\sqrt[2]{3})](/latexrender/pictures/399524712f54ca5abeea655608f31cf2.png)
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pessoa Estranha » Qua Set 18, 2013 20:52
por Pessoa Estranha » Qua Set 18, 2013 20:52
Olha, temos o seguinte:
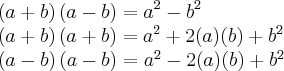
Lembra?
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Qua Set 18, 2013 21:00
por Pessoa Estranha » Qua Set 18, 2013 21:00
Você pode até fazer o processo da distributiva. Assim:
![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}}) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}})](/latexrender/pictures/8fc59f59a91c6ff5e46bdb52a93bb39d.png)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Vennom » Qua Set 18, 2013 23:19
por Vennom » Qua Set 18, 2013 23:19
Pessoa Estranha escreveu:Você pode até fazer o processo da distributiva. Assim:
![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}}) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}})](/latexrender/pictures/8fc59f59a91c6ff5e46bdb52a93bb39d.png)
Querida, se seguir a propriedade distributiva, o resultado não será exatamente o mesmo?
![6+\sqrt[2]{3} 6+\sqrt[2]{3}](/latexrender/pictures/f80cf9b7665bd683150468a02d903a05.png)
Me perdoe se eu realmente não estou conseguindo ver meu erro, mas insisto na gentileza sua de elucidá-lo para mim.
NOSSO DEUS, ME PERDOE,
MUITO OBRIGADO! VI MEU ERRO AGORA! HAHAHA, você está correta, Pessoa Estranha, foi jogo de sinal. Alí seria
![9-3-\sqrt[2]{3} 9-3-\sqrt[2]{3}](/latexrender/pictures/3eb686d0694193733895a86810393ebb.png)
Pura falta de atenção, realmente, muito obrigado pela sua gentileza em chamar minha atenção p/ o absurdo.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13778 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2241 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3438 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
-
- Meter dentro da raiz
por seixas » Seg Ago 22, 2011 13:58
- 2 Respostas
- 2167 Exibições
- Última mensagem por seixas

Seg Ago 22, 2011 17:15
Polinômios
-
- Raiz dentro de raiz
por zeramalho2004 » Seg Set 21, 2009 14:45
- 2 Respostas
- 19914 Exibições
- Última mensagem por Andre+

Ter Mar 23, 2010 21:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}}](/latexrender/pictures/1cec2a67a0cfed29fa364d9b4a198997.png)
![\sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}} \sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}}](/latexrender/pictures/23b21317c50f3e70e5ab9df2a471c2a4.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})}](/latexrender/pictures/d633042033fe640219efd61c667d9c49.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})}](/latexrender/pictures/da88b4ba4d376d828a6756b1bcef00b6.png) =>
=>![\sqrt[2]{63+27\sqrt[2]{3}} \sqrt[2]{63+27\sqrt[2]{3}}](/latexrender/pictures/b7a017c5ada2ba3e612a65df155868a7.png) =>
=>![3\sqrt[2]{5+\sqrt[2]{3}} 3\sqrt[2]{5+\sqrt[2]{3}}](/latexrender/pictures/5f5e7b6389df69bbadb03ae53a86535d.png) =>
=> ![\sqrt[2]{45+9\sqrt[2]{3}} \sqrt[2]{45+9\sqrt[2]{3}}](/latexrender/pictures/3604ee945cbe7386099ab0698c90c716.png)

![\sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3} \sqrt[2]{3+\sqrt[2]{3}} \sqrt[2]{3+\sqrt[2]{3+\sqrt[2]{3}}} \sqrt[2]{3-\sqrt[2]{3+\sqrt[2]{3}}}](/latexrender/pictures/1cec2a67a0cfed29fa364d9b4a198997.png)
![\sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}} \sqrt[2]{(3)(3+\sqrt[2]{3})(3+\sqrt[2]{3+\sqrt[2]{3})}(3-\sqrt[2]{3+\sqrt[2]{3})}}](/latexrender/pictures/23b21317c50f3e70e5ab9df2a471c2a4.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(9-3+\sqrt[2]{3})}](/latexrender/pictures/d633042033fe640219efd61c667d9c49.png) =>
=>![\sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})} \sqrt[2]{(9+3\sqrt[2]{3})(6+\sqrt[2]{3})}](/latexrender/pictures/da88b4ba4d376d828a6756b1bcef00b6.png) =>
=>![\sqrt[2]{63+27\sqrt[2]{3}} \sqrt[2]{63+27\sqrt[2]{3}}](/latexrender/pictures/b7a017c5ada2ba3e612a65df155868a7.png) =>
=>![3\sqrt[2]{5+\sqrt[2]{3}} 3\sqrt[2]{5+\sqrt[2]{3}}](/latexrender/pictures/5f5e7b6389df69bbadb03ae53a86535d.png) =>
=> ![\sqrt[2]{45+9\sqrt[2]{3}} \sqrt[2]{45+9\sqrt[2]{3}}](/latexrender/pictures/3604ee945cbe7386099ab0698c90c716.png)

![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right).\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)](/latexrender/pictures/e89eab6fc99912f4a593ad52552b441e.png)

![(9-3+\sqrt[2]{3}) (9-3+\sqrt[2]{3})](/latexrender/pictures/399524712f54ca5abeea655608f31cf2.png)

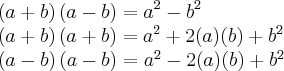

![\left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}}) \left(3+\sqrt[2]{3+\sqrt[2]{3}} \right)\left(3-\sqrt[2]{3+\sqrt[2]{3}} \right)=
{3}^{2}-3.\sqrt[2]{3+\sqrt[2]{3}}+3.\sqrt[2]{3+\sqrt[2]{3}}-(\sqrt[2]{3+\sqrt[2]{3}}.\sqrt[2]{3+\sqrt[2]{3}})](/latexrender/pictures/8fc59f59a91c6ff5e46bdb52a93bb39d.png)

![6+\sqrt[2]{3} 6+\sqrt[2]{3}](/latexrender/pictures/f80cf9b7665bd683150468a02d903a05.png)
![9-3-\sqrt[2]{3} 9-3-\sqrt[2]{3}](/latexrender/pictures/3eb686d0694193733895a86810393ebb.png)






