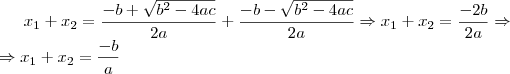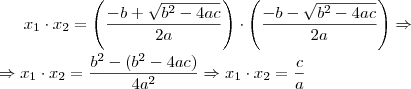- Voltei a resolver o "Matemática Paratodos 8º" e no capítulo sobre equações encontrei um dúvida. O livro coloca a seguinte questão (encontre o valorde 'x' para):
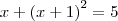
Resolução:

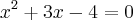
- O problema é o seguinte: Neste capítulo do livro, o aluno ainda não conhece a fórmula de Baskhara e esta estudando a resolução de equações do segundo grau apenas por fatoração (Isolando o fator comum ou determinando um trinômio quadrado perfeito, ou seja, produto notável que seja equivalente a expressão).
-Se eu tento resolver o produto notável (x+1)² e somo ele ao outro 'x', passando o '5' para este mesmo lado da igualdade (resultando em 'x²+3x-4=0'), não tenho mais como fatorar a equação (para usar a técnica do produto igual a zero). A não ser que eu já conheça as raizes da equação e aí então retroativamente estabeleça que:
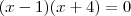
- O que por fatoração me parece a única forma de resolver a questão. Porém se eu chego a '-1' e '4' pela forma de baskhara em 'X²+3x-4' então esta resolção não fecha pq o aluno ainda não conhece a fórmula de baskhara.
Por favor alguém pode me dar uma luz? Se a multiplicação '(x-1)(x+4)' é a única fórma de resolver a equação sem usar baskhara, então como chegar a ela sem retroativamente usar baskhara para descobrir as raizes e estabelecer a multiplicação (afinal os números '-1' e '4' não saem do nada, não é mesmo? Existe uma técnica, não é?).
Grato, desde já. Abraços. Fui.


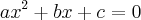 , então faça
, então faça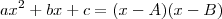

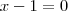 ou
ou 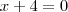 . Resolvendo
. Resolvendo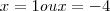

 , o que queremos é isolar a variável
, o que queremos é isolar a variável  , para isso vamos recorrer ao produto notável
, para isso vamos recorrer ao produto notável  . Aqui é sacada mais importante! Vc precisa dar um jeito de fazer isto:
. Aqui é sacada mais importante! Vc precisa dar um jeito de fazer isto: 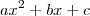 ser semelhante a isto:
ser semelhante a isto: 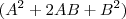 para daí poder tirar partido com a fatoração.
para daí poder tirar partido com a fatoração. , bem semelhante ao modelo da eq do 2º grau, não é mesmo? Agora vamos manipular o modelo para ficar mais semelhante ao produto notável...:
, bem semelhante ao modelo da eq do 2º grau, não é mesmo? Agora vamos manipular o modelo para ficar mais semelhante ao produto notável...: 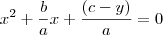 , pronto! Se identificarmos
, pronto! Se identificarmos 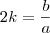 então
então 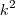 precisar ser
precisar ser 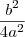 . É fácil ver que a parcela invariável do modelo não é igual a
. É fácil ver que a parcela invariável do modelo não é igual a 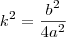 , o que fazemos então é rearrumar a expressão para que seja possível a fatoração, portanto:
, o que fazemos então é rearrumar a expressão para que seja possível a fatoração, portanto:  . Como
. Como  , então podemos fatorar o modelo já todo modificado e ficará assim:
, então podemos fatorar o modelo já todo modificado e ficará assim: 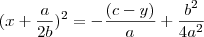 . Pronto! Agora está facinho de isolar a variável x, é só fazer isto e já era! Daí vc conhece o método de fatoração algébrico (superior ao numérico), que implica necessariamente na fórmula que não é de báscara, saberá resolver qualquer problema do 2º grau e poupará tempo com exercício picuinha.
. Pronto! Agora está facinho de isolar a variável x, é só fazer isto e já era! Daí vc conhece o método de fatoração algébrico (superior ao numérico), que implica necessariamente na fórmula que não é de báscara, saberá resolver qualquer problema do 2º grau e poupará tempo com exercício picuinha.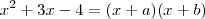
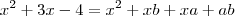
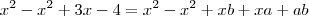

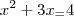

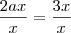
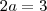
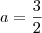
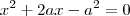
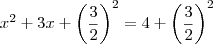
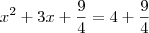
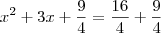
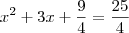
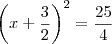
![x+\frac{3}{2}=\sqrt[]{\frac{25}{4}} x+\frac{3}{2}=\sqrt[]{\frac{25}{4}}](/latexrender/pictures/95d12431f91f7988e4bb0ccc0723aef6.png)
![x+\frac{3}{2}=\frac{\sqrt[]{25}}{\sqrt[]{4}}} x+\frac{3}{2}=\frac{\sqrt[]{25}}{\sqrt[]{4}}}](/latexrender/pictures/8aea3183457374cfe9c3918ce6880278.png)
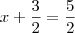
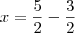
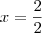

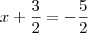
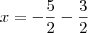


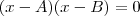 é fácil ver que as raízes são
é fácil ver que as raízes são  e
e  .
.
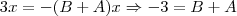
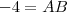
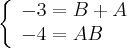
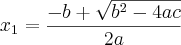
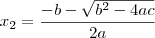
 com
com 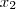 , teremos
, teremos