 por karine_ » Sáb Set 08, 2012 15:50
por karine_ » Sáb Set 08, 2012 15:50
Faltei a aula e não tenho nenhuma noção de resolver esse exercício, favor me ajudar!!!
1- Num sitio existe uma parede de tijolos q será utilizada como um dos lados de um cercadinho de formato retangular. Para construir os outros 3 lados será utilizada uma tela de 200m de comprimento.
a - faça o esboço do cercadinho visto de cima;
b- vc ainda ñ sabe as medidas dos lados, mas lhe foi solicitado escrever uma expressão p a área da figura retangular delimitada pela cerca sobre o solo. Escreva uma expressão p essa área;
c- escreva a expressão da área como uma função de apenas uma variável livre, levando em conta os 200m de tela;
d- calcule as medidas dos lados do cercadinho, de modo a obter a maior área interna possível;
e- calcule o valor dessa área máxima.
-
karine_
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Set 08, 2012 15:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: tec. meio ambiente
- Andamento: formado
 por young_jedi » Dom Set 09, 2012 17:59
por young_jedi » Dom Set 09, 2012 17:59
letra b ) como vc não sabe os qual sao as medias dos lados do cercadinho vc pode representa-lo por x e y
sendo assim uma expressão para a area seria

na letra c) tem que um dos lados é a parede então os outros tres lados serão formados pela tela como chamamos os lados
de x e y podemos dizer que y é o lado oposto a parede e x é a medidad dos outros dois lados
sendo assim temos que
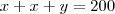
isolando y nesta expressão substitutindo na da area encontramos uma expressao para area apenas em função de x
letra d) a expressao da area encontrada deve ser uma equação do segundo grau portanto seu valor minimo esta no vertice da parabola com isto da pra determinar seu menor valor
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13238 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8720 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
-
- Equação - Problema
por ginrj » Qui Jun 11, 2009 15:52
- 5 Respostas
- 3406 Exibições
- Última mensagem por ginrj

Sáb Jun 13, 2009 18:34
Sistemas de Equações
-
- [ PROBLEMA ] Equação
por gabrielMAT » Qua Out 19, 2011 16:45
- 2 Respostas
- 1855 Exibições
- Última mensagem por gabrielMAT

Qua Out 19, 2011 19:58
Sistemas de Equações
-
- Problema de equação
por TiagoFERD » Sáb Mar 10, 2012 09:59
- 2 Respostas
- 1447 Exibições
- Última mensagem por TiagoFERD

Sáb Mar 10, 2012 10:48
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



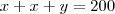



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.