por Valmel » Ter Out 23, 2012 18:23
31)Para enumerar as páginas de um livro foram necessários 1296 algarismos.Calcule quantas páginas tem esse livro.
1) Acho que começa assim,de 1 ao 9,eu usei 9 paginas;
2)De 10 a 99,eu usei 90 paginas;
Não estou conseguindo desenrolar...
-
Valmel
- Usuário Ativo
-
- Mensagens: 20
- Registrado em: Qui Set 27, 2012 17:59
- Localização: Ceará
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
por young_jedi » Ter Out 23, 2012 19:56
pense no seguinte o numero das paginas de um livro tem algarismos da unidade, da dezena e das centenas
todas as paginas tem o algarismo das unidades, se o total de paginas é x então ele possui x algarimos da unidade
as nove primeiras paginas do livro nao possuem o algarismo das dezenas portanto a quantidade total de algarismo das dezenas é x-9
as 99 primeiras paginas do livro nao possuem o algarismo das centenas portanto a quantidade total de algarimos das centenas é x-99
portanto a quantidade total de algarismo é
resolvendo se encontra x.
-
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ALGARISMOS DE 0 A 9
por Molina » Dom Jun 12, 2011 22:35
- 8 Respostas
- 6769 Exibições
- Última mensagem por tenebroso
Qua Dez 18, 2013 23:18
Desafios Difíceis
-
- algarismos!!!
por alissonade » Sex Abr 26, 2013 23:38
- 5 Respostas
- 3836 Exibições
- Última mensagem por alissonade
Dom Abr 28, 2013 19:10
Aritmética
-
- Soma dos algarismos
por thadeu » Qua Nov 18, 2009 16:19
- 4 Respostas
- 2547 Exibições
- Última mensagem por thadeu
Qua Nov 18, 2009 20:01
Álgebra Elementar
-
- Quantidade de Algarismos
por gustavowelp » Seg Jul 18, 2011 00:20
- 6 Respostas
- 4000 Exibições
- Última mensagem por Molina
Seg Jul 18, 2011 11:42
Estatística
-
- soma dos algarismos
por gokeafro » Sex Out 14, 2011 18:22
- 0 Respostas
- 1446 Exibições
- Última mensagem por gokeafro
Sex Out 14, 2011 18:22
Sistemas de Equações
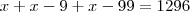
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
