Paulo misturou um líquido A com um líquido B em igual quantidade, obtendo 15 litros. Para obter uma nova mistura com 2/7 do líquido A, Paulo deverá acrescentar à mistura
A) 9 litros do líquido B.
B) 12 litros do líquido B.
C) 3 litros do líquido A e 12 litros do líquido B.
D) 1,5 litro do líquido A e 15 litros do líquido B.
Fiz assim:
A+B = 15
A e B possuem quantidades iguais.
15/2 = 7,5
A = 7,5 e B= 7,5
Nova mistura:
2a/7 = (2 * 7,5)/7 = 15/7
Daqui por diante tenho dúvida...
Seria (15/7) + B = X ????
15/7 + 7,5 = X ????
Alguém pode me ajudar?


 . Para mudarmos esta proporção teremos que descobrir o que teremos que adicionar.
. Para mudarmos esta proporção teremos que descobrir o que teremos que adicionar. e sendo este número menor do que 50%, vemos que temos que 'retirar' líquido A da proporção, o que não é viável, ou adicionar líquido B de forma a deixar a proporção para o outro líquido menor.
e sendo este número menor do que 50%, vemos que temos que 'retirar' líquido A da proporção, o que não é viável, ou adicionar líquido B de forma a deixar a proporção para o outro líquido menor.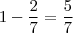
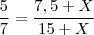 , sendo X o valor de líquido B a ser acrescentada.
, sendo X o valor de líquido B a ser acrescentada.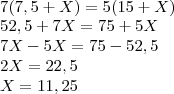
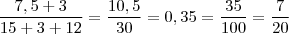
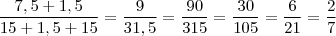
 )
)


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.