Olá a todos.
Desejava ajuda para a seguinte questão.
Dois números do sistema decimal representam-se por 7 e 4 = 74, em dois sistemas cujas bases diferem entre si de três unidades. Sabendo que a soma dos referidos números em decimal é 99, determinar aquelas outras duas bases.
Sei que a solução é: 5 e 8.
Mas gostaria de saber como equacionar o problema para chegar nas ditas soluções.
Grato a quem resolver ou apontar um bom método de resolução.
Armando


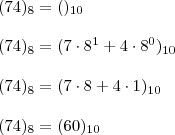
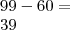


 .
.
 :
: