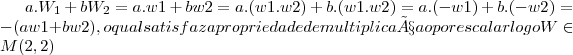por Nicolas1Lane » Sex Set 12, 2014 16:45
por Nicolas1Lane » Sex Set 12, 2014 16:45
A questão que estou a fazer me pede para verificar se W é subspaço de M(2,2) sendo W

M(2,2)/ b = a d = -a
Então pensei; fácil, basta provar que as propriedades de soma de 2 matrizes estão contidas no subespaço assim como o produto de 2 matrizes igual ao produto do mesmo quando sua ordem for trocada...
-Para a soma, Ok.
-Mas para o produto, nem
Queria ajuda de vocês para ver se estou certo nisto ou o gabarito está correto. Ele afirma ser verdade que W é subspaço de M.
Mas olhem comigo isto:
Se
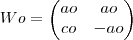
e
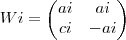
Então
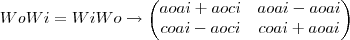
=
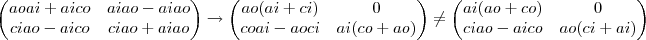
Poderiam me dar uma luz, galera?
-
Nicolas1Lane
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Set 11, 2013 23:25
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: Exatas/Ciência da Computação
- Andamento: cursando
 por adauto martins » Qui Out 23, 2014 15:11
por adauto martins » Qui Out 23, 2014 15:11
para provar se W e um subespaço,deve-se provar q.:
1)
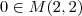
:
afirmativo,pois 0=0.0=-0,logo
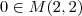
2)dados
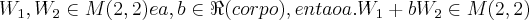
,aqui multiplicaçao por escalar e nao multiplicaçao de matruizes,como vc fez,entao:
sejam...
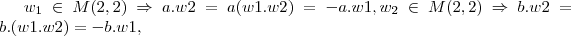
,LOGO:
a.
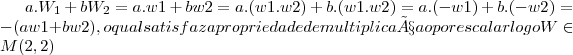
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Álgebra linear - Subespaço Gerado
por nietzsche » Sex Jan 06, 2012 19:48
- 2 Respostas
- 1916 Exibições
- Última mensagem por nietzsche

Ter Jan 10, 2012 17:16
Álgebra Linear
-
- [Álgebra Linear] Ache a dimensão do subespaço...
por gabriel17carmo » Sex Jun 08, 2012 23:16
- 5 Respostas
- 3894 Exibições
- Última mensagem por gabriel17carmo

Seg Jun 11, 2012 02:42
Álgebra Linear
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10991 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4691 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- subespaço
por alzenir agapito » Qui Jul 21, 2011 17:52
- 0 Respostas
- 1782 Exibições
- Última mensagem por alzenir agapito

Qui Jul 21, 2011 17:52
Álgebra
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 M(2,2)/ b = a d = -a
M(2,2)/ b = a d = -a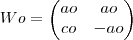 e
e 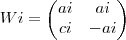
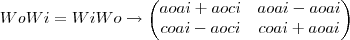 =
= 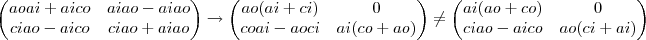


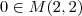 :
: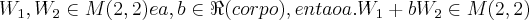 ,aqui multiplicaçao por escalar e nao multiplicaçao de matruizes,como vc fez,entao:
,aqui multiplicaçao por escalar e nao multiplicaçao de matruizes,como vc fez,entao: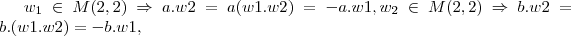 ,LOGO:
,LOGO: