[transformações lineares] matriz do operador

[Tathiclau]

Determine a matriz do operador T : R² -> R² relativamente a base  a = (1, 1), (-1, 1),
sabendo que T(-7, 4) = (2, 3) e T(6, 1) = (4, 5).

[e8group]

Acho que queria dizer . A primeira coisa que deve se perguntar o conjunto 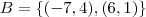é L.I. ? R. sim é L.I. e não é necessário tomar combinação linear nula, basta notar que eles não são múltiplos escalares . Segundo , através de um resultado da A.L. vide viewtopic.php?f=117&t=13470 , podemos afirmar que constitui uma base ordenada para o 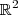.Como sabemos o que o operador 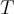faz com os vetores de B ,é possível determina-lo (basta reescrever (x,y) como combinação linear dos vetores de B e em seguida aplicar o operador T e usar a linearidade dele ) .
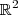Em resumo , para este exercício apenas precisávamos verificar se B é uma base p/ ,como ele é , então deverás escrever 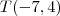e como combinação linear dos vetores de .

Espero que ajude .