 por lucasdemirand » Sáb Jul 06, 2013 16:47
por lucasdemirand » Sáb Jul 06, 2013 16:47
olá pessoal, aí vai uma duvida em algebra, grato a quem puder ajudar
dado o triangulo de vértices A(1,2,1), B (3,-1,7) e C(7,4-2), mostrar que o triangulo é isoceles e determinar o ângulo interno do vértice A.
-
lucasdemirand
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sáb Jul 06, 2013 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por nakagumahissao » Qua Out 07, 2015 20:08
por nakagumahissao » Qua Out 07, 2015 20:08
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7470 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3219 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2753 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2717 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2662 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



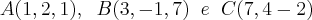
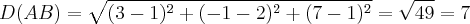
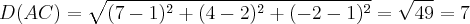
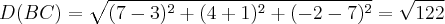
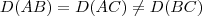
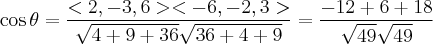
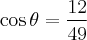
![\theta = \arccos \left[\frac{12}{49} \right] = 75,82 \theta = \arccos \left[\frac{12}{49} \right] = 75,82](/latexrender/pictures/7a4e5b6e801d18add9cf0d298c90250c.png)

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.