Determinar um vetor unitário do
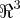que seja ortogonal a todos os vetores do subespaço ![W = \left[(1, 2, -1),(-1,0,2) \right]](/latexrender/pictures/94e9e1665fb21b722e5ec64421883f53.png "W = \left[(1, 2, -1),(-1,0,2) \right]")
.Para fazermos isto, precisamos, primeiro, encontrar uma base ortonormal para W. Consegui encontrá-la através do Processo de Gram-Schmidt. Seja B essa base. Segue:
![B = \left(\frac{1}{\sqrt[]{6}}(1,2,-1), \frac{1}{\sqrt[]{14}} (-1,2, 3) \right)](/latexrender/pictures/589209f2c76bca0cde21e0b5376a8ca2.png "B = \left(\frac{1}{\sqrt[]{6}}(1,2,-1), \frac{1}{\sqrt[]{14}} (-1,2, 3) \right)")
. Daí, temos um resultado que garante-nos que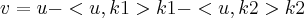 
é o vetor ortogonal a todos os elementos de W, onde 
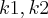são os elementos da base B e, u é um vetor qualquer de W, u = (a, b, c), por exemplo. Porém, eu simplesmente não consigo chegar ao resultado! Obtive umas frações com numeradores e denominadores gigantes! Por favor, preciso muito de ajuda!!!!Muito Obrigada!
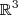que é um plano que passa pela origem gerado pelos vetores 
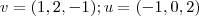.Pois bem , da G.A. sabemos que o produto vetorial entre u e v( 
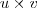) é ortogonal ao plano em questão , i.e, ele é ortogonal a todos vetores de W . E por fim concluímos que qualquer vetor que está na mesma direção de 
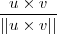ou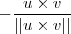 
. Fazendo as contas , vc tem qu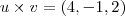e 
e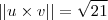 
....
.
: