 por will140592 » Dom Mar 03, 2013 11:40
por will140592 » Dom Mar 03, 2013 11:40
dada a equaçao x+6=x²,uma equaçao equivalente a mesma é:
resposta que eu achei que poderia ser: c) x+6+[(1)/(x-3)]=x²+[(1)/(x-3)]
resposta certa de acordo com o livro: d) 3(x+6)=3x²
duvida: na resposta c exite uma fraçao igual nos dois lado da equaçao, por que eu nao poderia cancelar, assim a equaçao ficaria igual.
-
will140592
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 03, 2013 11:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Russman » Dom Mar 03, 2013 19:45
por Russman » Dom Mar 03, 2013 19:45
Note que

é raíz da equação. Assim, a fração
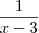
iria gerar

descartando essa solução. Por isso que a forma proposta para a equação não é bem vista mesmo que, sim, você pudesse cancelar as frações em ambos membros da equação.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3894 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Equação de segundo grau
por maria cleide » Seg Mai 09, 2011 23:46
- 3 Respostas
- 2694 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 10, 2011 00:43
Sistemas de Equações
-
- Equação do segundo grau
por LuizCarlos » Qui Mai 10, 2012 13:01
- 3 Respostas
- 3112 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 12, 2012 20:41
Álgebra Elementar
-
- Equação do segundo grau
por LuizCarlos » Sex Jun 15, 2012 16:14
- 5 Respostas
- 3751 Exibições
- Última mensagem por LuizCarlos

Sáb Jun 16, 2012 13:31
Álgebra Elementar
-
- equaçao de segundo grau
por will140592 » Dom Mar 03, 2013 20:21
- 1 Respostas
- 1825 Exibições
- Última mensagem por Russman

Dom Mar 03, 2013 20:43
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 é raíz da equação. Assim, a fração
é raíz da equação. Assim, a fração 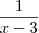 iria gerar
iria gerar  descartando essa solução. Por isso que a forma proposta para a equação não é bem vista mesmo que, sim, você pudesse cancelar as frações em ambos membros da equação.
descartando essa solução. Por isso que a forma proposta para a equação não é bem vista mesmo que, sim, você pudesse cancelar as frações em ambos membros da equação.

 .
.



