2.mostre que o conjunto de combinações lineares das variáveis x e y é um espaço vetorial com operações usuais
Combinações lineares de x e y formam o conjunto dos elementos u = ax + by
A1 associativa u + (v + w) = (u + v) + w
ax + by + (cx + dy + ex + fy) = ax + by + cx + dy + ex + fy = (ax + by + cx + dy) + ex + fy
Alguém pode me ajudar? Gostaria de saber se estar correto, e quais passos devo seguir. ( Estou estudando por conta, e sou leiga)


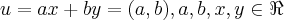 }
}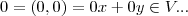 e p/quaquer
e p/quaquer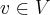
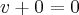
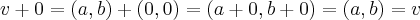
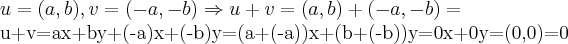
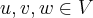
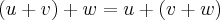
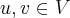
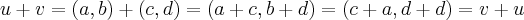
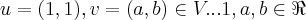
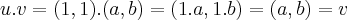
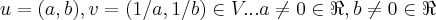
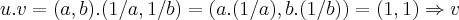 é o elemento inverso multplicativo de u...
é o elemento inverso multplicativo de u...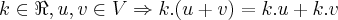

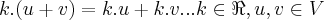
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.