Ola pessoal!
Estou com dúvidas para resolver a seguinte questão.
O capital de $ 2.500, é aplicado durante 4 meses a juros compostos produzindo o montante de $ 3.500,.
(1) Calcular a taxa mensal de Juros Compostos
(2) Qual a taxa de Juros Simples necessária para o referido capital produzir o mesmo montante no prazo considerado?
Gabarito =
(1) i = 8,776% a.m. (JC)
(2) i = 10% a.m. (JS)
Segue a forma como resolvi....


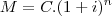 ... substituindo....
... substituindo.... 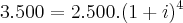

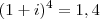
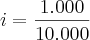



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.