Manoella escreveu:Alguém poderia mim indicar como vou fazer para calcular esse problema?
Uma pessoa comprou uma maquina nas seguintes condições: 2 000,00 tres meses após a compra seguidas de mais 2 prestações mensais no valor de 1 500,00 cada uma.Sabendo -se que a taxa de juros nominal usada foi de 24% ao ano, capitalizada mensalmente, encontre o valor a vista da maquina?
Eu faria assim, quem puder ajudar criticando, será de muito boa chegada. Não sei estou certo. Chamemos de 'x' o valor procurado.
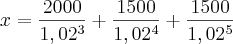
O denominador 1,02 é 24%aa, divididos por 12, transformado em taxa unitária e somando 1. A taxa anual é nominal, apenas para referência, e a taxa para efetivo cálculo é sua representação em meses, já que os períodos são dados ao mês.
Cada fração é uma descapitalização parcial de uma das prestações até a data inicial. É decorrente da transformação algébrica da fórmula do Montante.
Somando os valores encontrados de cada prestação no dia de partida do financiamento, teremos
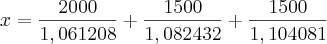
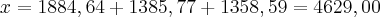


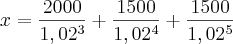
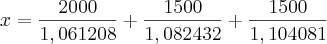
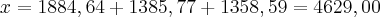
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)