 por claudiosantos35 » Ter Mai 24, 2011 16:12
por claudiosantos35 » Ter Mai 24, 2011 16:12
Segundo informações da Sabesp, até 2 anos de idade, 80% do nosso corpo é formado de água; aos 5 anos, essa porcentagem cai para 70% até que, depois dos 60 anos, temos apenas 58% de água no organismo.
Nessas condições, uma pessoa com mais de 60 anos tem, em relação à quantidade de água no organismo que possuía aos 2 anos de idades, uma redução de x% de água. O valor de x é:
Alternativa A = 23,5
Alternativa B = 24,0
Alternativa C = 25,5
Alternativa D = 26,0
Alternativa E = 27,5
Nota: Eu sei que a resposta para essa pergunta é a alternativa E, mas eu necessito saber como chegar a esse resultado.
-
claudiosantos35
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mai 20, 2010 16:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: biologia
- Andamento: formado
 por arpavan » Qua Mai 25, 2011 17:43
por arpavan » Qua Mai 25, 2011 17:43
Olá Claudio
uma fórmula simples para calcular taxas de crescimentos entre valores:
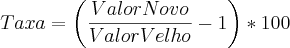
No teu problema, os valores são tratados como se a porcentagem fosse uma simples unidade:
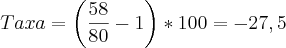
o o sinal negativo indica um decrescimento entre os dados.
então, a resposta é:
uma pessoa tem uma redução de 27,5% de água aos 60 anos, em relação ao que possuía aos 2 anos.
Até mais.
Professor Alcione Rafael
Professor Alcione Rafael PavanGraduado, Licenciatura em Matemática e Mestre em Modelagem Matemática
Disciplinas que trabalho: Matemática Aplicada, Matemática Financeira, Cálculo I, Cálculo Numérico, Estatística I, Estatística II , Pesquisa Operacional, Informática Básica
Cursos que Ministro: Matemática Financeira com HP12C, Excel Básico e Excel Avançado
http://www.arpavan.com
-
arpavan
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mai 25, 2011 17:32
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestre em Modelagem Matemática
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Porcentagem] Fração mista e porcentagem
por Mayra Luna » Ter Fev 26, 2013 20:58
- 2 Respostas
- 4580 Exibições
- Última mensagem por Mayra Luna

Ter Fev 26, 2013 23:41
Álgebra Elementar
-
- Porcentagem - Porcentagem com minutos
por marcorrer » Qua Abr 04, 2012 13:52
- 6 Respostas
- 7910 Exibições
- Última mensagem por marcorrer

Seg Abr 09, 2012 16:25
Álgebra Elementar
-
- Porcentagem
por Danilo Dias Vilela » Qui Set 10, 2009 22:31
- 1 Respostas
- 3750 Exibições
- Última mensagem por Molina

Sex Set 11, 2009 14:22
Matemática Financeira
-
- Porcentagem
por Danilo Dias Vilela » Sex Set 11, 2009 18:09
- 2 Respostas
- 3682 Exibições
- Última mensagem por Danilo Dias Vilela

Sex Set 11, 2009 21:17
Matemática Financeira
-
- Porcentagem
por matematicando » Ter Set 15, 2009 12:52
- 0 Respostas
- 2919 Exibições
- Última mensagem por matematicando

Ter Set 15, 2009 12:52
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


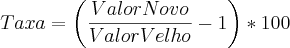
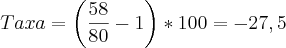

 .
.



