Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Neperiano » Qua Fev 11, 2009 18:32
por Neperiano » Qua Fev 11, 2009 18:32
Ola
Como prometi vou postar aqui algumas questões do Vestibular 2008 da UFRGS, terceiro melhor do Brasil, cuja prova de Matemática é considerada a mais Dificel.
Ai vai:
1 - O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar. Se o custo para embalar um cubo de 40 cm de aresta é R$10,00, a embalagem de um cubo de 80 cm de aresta custa, em reais,
(A) 15.
(B) 20.
(C) 25.
(D) 40.
(E) 80.
2 - Em março de 2007, o menor preço oferecido por uma companhia telefônica para uma ligação do Brasil para os Estados Unidos era de R$0,95 o minuto. O mesmo serviço pela internet custava R$0,05 o minuto e mais R$0,10 da taxa de conexão da chamada. Em ambas as situações, o preço por segundo correspondia a do preço por minuto.
Nessas condições, para que uma ligação telefônica, do Brasil para os Estados Unidos, tivesse um custo menor via companhia telefônica do que via internet, a duração dessa ligação deveria ser, em número inteiro de segundos, no máximo, de
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.
3 - Um hexágono regular tem lado de comprimento 1. A soma dos quadrados de todas as suas diagonais é
(A) 6.
(B) 12.
(C) 18.
(D) 24.
(E) 30.
4 - Numa seqüência de quadrados, o primeiro tem lado igual a 1, e o lado de cada um dos seguintes é igual à diagonal do quadrado anterior.
A soma das áreas dos dez primeiros quadrados dessa seqüência é
(A) 1023.
(B) 1024.
(C) 2047.
(D) 2048.
(E) 4096.
5 - O polinômio p(x)=

tem
(A) apenas duas raízes reais distintas.
(B) apenas duas raízes positivas.
(C) todas as raízes positivas.
(D) quatro raízes iguais.
(E) quatro raízes distintas.
6 - Traçando-se os gráficos das funções definidas por f(x) = 2 sen x e g(x) = 16 -

e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sáb Fev 14, 2009 05:11
por Molina » Sáb Fev 14, 2009 05:11
Boa noite, Maligno.
Como o pessoal aqui não anda com muito tempo para resolver essas questões, vou postar a solução (de todas que eu conseguir resolver):
1) Essa questão te induz a pensar que duplicando a aresta do cubo a área da superfície duplicará também. Isto não é verdade. Neste caso um cubo de 40cm de aresta tem superfície de 9600cm² (custando R$ 10,00) e um cubo de 80cm de aresta tem superfície de 38400cm², que é o quádruplo de 9600cm², ou seja, o valor deve ser multiplicado por 4 também. Com isso concluimos que custará
R$ 40,00.
2) Verificar quanto é o gasto por segundo dos dois modos de comunicação:
Telefone = 1,58333 centavos por minuto
Internet = 0,08333 centavos por minuto (porém pága-se 10 centavos da taxa)
Ou seja, utilizando 1 segundo o telefone eu gastaria apenas 1,58333 centavos e utilizando 1 segundo a internet eu gastaria 10,08333. O maior número que posso multiplicar 1,58333 para ser menor que 10,08333 é
6:
1,58333 *
6 = 9,49998 < 10,08333
1,58333 * 7 = 11,08331 > 10,08333
3) Um hexágono regular possui 3 diagonais. A diagonal de um hexágono regular é 2 vezes o tamanho do raio de um circulo circunscrito nesse polígono. O lado de um hexágono regular é igual ao raio de um circulo circunscrito nesse hexágono: LADO = RAIO (formando 6 triângulos equiláteros dentro do hexágono).
Lado = 1

Raio = 1

Diagonal = 2

2² + 2² + 2² =
124) Primeiramente quando li achei que seria o problema mais difícil dessa lista. Mas não, é bem simples: Começando pelo primeiro quadrado de lado 1, tem-se área igual a 1 também. Lembre-se da fórmula da diagonal do quadrado, dada por
![D = \ell\:\sqrt[]{2} D = \ell\:\sqrt[]{2}](/latexrender/pictures/777e9f39975a29b503809d772846b527.png)
. Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de
1023.
5)



6) Construi o gráfico das duas, e se não errei na contrução deles eles terão apenas
2 pontos onde f(x) = g(x).
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por FilipeCaceres » Sex Mai 13, 2011 01:24
por FilipeCaceres » Sex Mai 13, 2011 01:24
Considerando que

seja
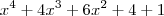
então é fácil perceber que:
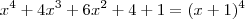
Portanto,as quatro raízes iguais.
Resposta:
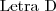
.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por rcompany » Qui Fev 21, 2019 23:21
por rcompany » Qui Fev 21, 2019 23:21
1 - O custo de uma embalagem é diretamente proporcional à superfície do sólido que se deseja embalar. Se o custo para embalar um cubo de 40 cm de aresta é R$10,00, a embalagem de um cubo de 80 cm de aresta custa, em reais,
(A) 15.
(B) 20.
(C) 25.
(D) 40.
(E) 80.
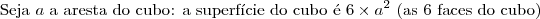
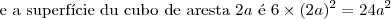

2 - Em março de 2007, o menor preço oferecido por uma companhia telefônica para uma ligação do Brasil para os Estados Unidos era de R$0,95 o minuto. O mesmo serviço pela internet custava R$0,05 o minuto e mais R$0,10 da taxa de conexão da chamada. Em ambas as situações, o preço por segundo correspondia a do preço por minuto.
Nessas condições, para que uma ligação telefônica, do Brasil para os Estados Unidos, tivesse um custo menor via companhia telefônica do que via internet, a duração dessa ligação deveria ser, em número inteiro de segundos, no máximo, de
(A) 6.
(B) 7.
(C) 8.
(D) 9.
(E) 10.

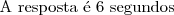
3 - Um hexágono regular tem lado de comprimento 1. A soma dos quadrados de todas as suas diagonais é
(A) 6.
(B) 12.
(C) 18.
(D) 24.
(E) 30.

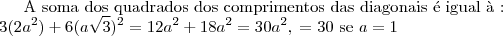
4 - Numa seqüência de quadrados, o primeiro tem lado igual a 1, e o lado de cada um dos seguintes é igual à diagonal do quadrado anterior.
A soma das áreas dos dez primeiros quadrados dessa seqüência é
(A) 1023.
(B) 1024.
(C) 2047.
(D) 2048.
(E) 4096.


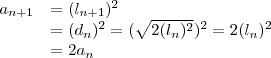

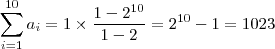
5 - O polinômio p(x)=

tem
(A) apenas duas raízes reais distintas.
(B) apenas duas raízes positivas.
(C) todas as raízes positivas.
(D) quatro raízes iguais.
(E) quatro raízes distintas.
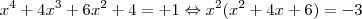
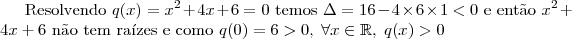
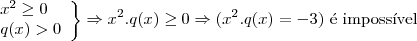
Mas achei o texto original e aí fica mais fácil ainda:

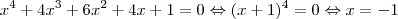
6 - Traçando-se os gráficos das funções definidas por
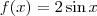
e
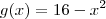
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
(A) 0.
(B) 1.
(C) 2.
(D) 3.
(E) 4.
![\phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0 \phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0](/latexrender/pictures/56cd4f5842222ffa3cf56bea01e2a9e4.png)
![\left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right \left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right](/latexrender/pictures/e541cc339277324141018ac2a21491d7.png)
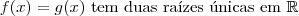
-
rcompany
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Seg Fev 18, 2019 00:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: administração
- Andamento: formado
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ufrgs
por Maria Livia » Seg Mar 18, 2013 19:18
- 3 Respostas
- 4805 Exibições
- Última mensagem por timoteo

Qua Mar 20, 2013 11:36
Geometria Plana
-
- ufrgs
por Maria Livia » Ter Set 03, 2013 12:41
- 1 Respostas
- 5558 Exibições
- Última mensagem por MateusL

Qua Set 04, 2013 11:20
Trigonometria
-
- (UFRGS)Quadrilátero
por flavio2010 » Sex Jul 16, 2010 06:36
- 1 Respostas
- 2030 Exibições
- Última mensagem por Douglasm

Sex Jul 16, 2010 21:08
Geometria Plana
-
- (UFRGS) Complexo
por flavio2010 » Sáb Jul 17, 2010 12:51
- 1 Respostas
- 2065 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 14:10
Números Complexos
-
- Função UFRGS
 por Kelvin Brayan » Ter Mai 24, 2011 18:47
por Kelvin Brayan » Ter Mai 24, 2011 18:47
- 3 Respostas
- 7879 Exibições
- Última mensagem por Kelvin Brayan

Qua Mai 25, 2011 00:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tem
tem e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é

 Raio = 1
Raio = 1 ![D = \ell\:\sqrt[]{2} D = \ell\:\sqrt[]{2}](/latexrender/pictures/777e9f39975a29b503809d772846b527.png) . Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de
. Logo você percebe que a área do segundo quadrado é 2, do terceiro é 4, do quarto é 8, ... , caindo numa PG de razão 2. Usando a fórmula da soma de uma PG finita chega-se ao resultado de 

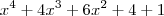 então é fácil perceber que:
então é fácil perceber que: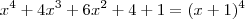
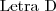 .
.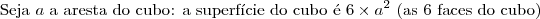
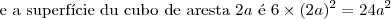


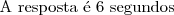

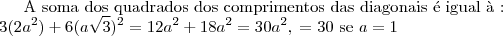


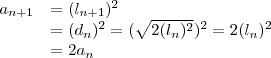

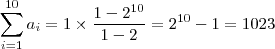
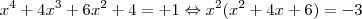
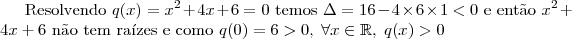
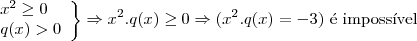

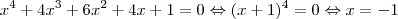
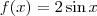 e
e 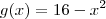 e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é
e num mesmo sistema de coordenadas cartesianas ortogonais, pode-se verificar que o número de soluções da equação f(x) = g(x)é![\phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0 \phi(x)=x^2+2\sin{x}-16\\
\phi'(x)=2x+2\cos{x}\\
\phi''(x)=2-2\sin{x} \Rightarrow \forall x \in \mathbb{R},\;\phi''(x)\geq 0 \; \Rightarrow \phi' \text{ \'e crescente}\\
\left\!\!\!\!\begin{array}{r}\phi'\text{estr.crescente, continua sobre }[-\frac{\pi}{2};0]\\ \phi'(-\frac{\pi}{2})=-\pi\\ \phi'(0)=2 \end{array}\!\!\!\right\}\!\!\!\Rightarrow \!\!\exists\alpha\!\!\in ]\frac{-\pi}{2};0[\text{\'unico tal que }\phi'(\alpha)=0 \\
\phi \text{ decrescente em }]-\infty;\alpha]\text{ e crescente em }[\alpha;+\infty[\\
\phi'(\alpha)=0\Rightarrow \alpha=-\cos{\alpha}\Rightarrow \phi(\alpha)=\cos^2{\alpha}+2\sin{\alpha}-16=-\sin^2{\alpha}+2\sin{\alpha}-15\\
\text{Seja }t=\sin{\alpha}\text{ vemos que }-t^2+2t-15=0 \text{ n\~ao tem ra\'izes e } -t^2+2t-15<0\\
\text{ou seja }\phi(\alpha)<0](/latexrender/pictures/56cd4f5842222ffa3cf56bea01e2a9e4.png)
![\left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right \left \begin{array}{r}\phi\text{ continua sobre }\mathbb{R}\\
\phi\text{ estritamente decrescente sobre }]-\infty;\alpha[\\
\phi\text{ estritamente crescente sobre }]\alpha;+\infty[\\
\phi(-2\pi)>0 ,\phi(\alpha)<0,\phi(2\pi)>0 \end{array}\right \} \Rightarrow\left \{ \begin{array}{l}\exists x_1 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_1)=0\\
\exists x_2 \text{\'unico } \in ]-2\pi;\alpha[ \text{ tal que } \phi(x_2)=0\\
\forall x < -2\pi \text{ ou }x>2\pi,\;\phi(x)>0 \end{array}\right](/latexrender/pictures/e541cc339277324141018ac2a21491d7.png)
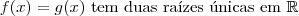



 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
