Provar Propriedade Arquimediana: Para qualquer real x existe n E N/n>x
Podemos provar por absurdo por exemplo:
Se para algum x E R tivéssemos n<x, para todo n E N, então x é uma cota superior de N.
Como podemos provar isso passo a passo?
Grato!
por Jovani Souza » Sáb Mai 18, 2013 12:32
por e8group » Sáb Mai 18, 2013 16:52
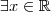tal que 
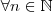tem-se 
então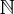 
é limitado superiormente e possui uma cota superior .Consideremos
a menor das cotas superiores .Como o número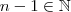 
e 
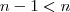implica que este número não é limite superior de 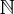.Assim , 
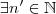tal que 
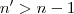o que implica 
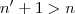.Como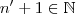 
,concluímos não é majorante e também não pode ser a menor das cotas superiores de 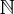e isto é uma contradição ,uma vez que consideremos como a menor das cotas superiores .Desta forma ,concluímos que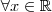 
sempre existirá algum número natural 
.
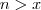Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)