Estive pensando... se existe média artimética definida como
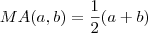, se existe média geométrica definida como 
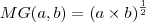e se existe média harmônica (que é essencialmente do tipo aritmética, só que inversa) definida como 
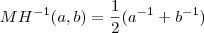... ENTÃO pq "não existe" a média harmônica do tipo geométrica 
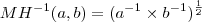?Apesar de estar discutindo sobre a "harmonidade" das médias eu não sei pq certas expressões matemática são qualificadas em harmônicas ou desarmônicas, o que isto significa?
Ademais, eu já li e pesquisei sobre média harmônica na internet, porém ainda não entendi o que ela faz e para que ela serve, gostaria de maiores esclarecimentos!
Grato!
por 
.
: